확률변수와 관련된 Jensen의 부등식을 예를 이용하여 직감적으로 이해해보려고 한다.
x를 확률 변수, p(x)를 x의 확률밀도함수라고 한다면 그 기대치 E[x]는 아래의 식과 같다.

이때 위에 볼록 튀어나온 함수 f(x)에 대해,

위의 부등식이 성립한다면, "Jensen의 부등식"이라고 부른다. 이 증명과 관련하여는 여러 곳에서 해설하고 있으니 여기서는 생략하고 하도록 한다. (예를 들면, 여기)
이 부등식 f(E[x])≥E[f(x)] 을 직감적으로 이해하기 위해 난수를 이용한 예를 그래프로 표시해보도록 하겠습니다.
먼저, x가 정규분포를 따르는 확률 변수라고 가정했을 때, 여기서 발생하는 난수를 만들어 보았습니다. 또한, x를 아래의 함수로 변환하였습니다.
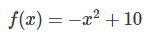
아래의 그래프 위쪽에 있는 히스토그램이 정규분포에 따른 x의 분포이고, 오른쪽의 히스토그램은 x 제곱에 따른 분포이다.
즉, 옌센 부등식은 아래의 빨간 동그라미(기대치를 얻은 후 즉 위의 히스토그램에서 평균을 얻은 후 f(x)에 의해 변환된다)의 쪽이 녹색은 동그라미 (f(x)로 변환된 후 기대치를 얻는다, 즉 오른쪽의 히토그램의 평균치) 보다 크다는 것을 나타내고 있다.

x의 분포가 어떤 정규분포의 평균을 조금씩 미뤄가며 애니메이션화시켜 본 것이 아래와 같다. 어떠한 경우에서도 녹색의 동그라미가 빨간 색 동그라미보다 아래에 있다는 것을 알 수 있다.

그렇다면 이 부등식의 좋은 점은 무엇일까?
옌센부등식(아래의 식)은

f(E[x])를 최대화하고 싶지만, 그 함수로 무엇이 있을지 불명확할 때, E[f(x)]로 계산할 수 있다면 E[f(x)]가 f(E[x])의 아래 쪽 한계(=하한)으로 생각할 수 있으므로 계산 가능한 E[f(x)]를 최대화하여 원래의 목표인 f(E[x])를 최대화 하는 것이다.
자주 사용되는 것은 log(⋅)로 위에 블록한 함수가 되므로 아래와 같이 log(⋅)를 적분에 넣어서 계산할 수 있도록 하겠다는 것이다.

조금 알기 힘든 설명이 되어버렸지지만, log(⋅)의 경우의 애니메이션을 살펴보자.
오른쪽의 히스토그램을 보면 아래쪽이 일그러져 있으므로 평균치가 아래로 어긋나는 것을 감각적을 알 수 있다. 그 만큼, 녹색의 동그라미가 빨간색 동그라미보다 아래에 있다는 것을 알 수 있다.

이 포스팅에 쓴 python 코드는 아래의 링크를 참고해주길 바란다.
https://github.com/matsuken92/Qiita_Contents/blob/master/General/Jensens-inequality.ipynb
matsuken92/Qiita_Contents
This is a repository for submitted contents of Qiita. - matsuken92/Qiita_Contents
github.com
참고 자료
'IT > AI\ML' 카테고리의 다른 글
| [논문] 최근 AI의 이미지 인식에서 화제인 "Vision Transformer"에 대한 해설 (0) | 2020.10.16 |
|---|---|
| [수학/분포] 정규분포 간의 KL 발산(쿨백-라이블러 발산 ; Kullback–Leibler divergence, KLD) (0) | 2020.08.07 |
| GAN ; PG-GAN(Progressive Growing of GANs) (0) | 2020.07.06 |
| 머신러닝 분류 모델의 성능평가 (0) | 2020.05.27 |
| [python] 머신러닝의 모델 정밀도 향상에 효과적인 학습곡선과 검증곡선 입문 (0) | 2020.05.25 |