인공지능을 학습시키는 것까지는 좋았으나 '전혀 사용할 수 없잖아!'라고 생각되는 과학습에 빠져버리면 곤란하다. 과학습이란 훈련 데이터(학습 데이터)는 정답은 잘 맞추지만 미지의 데이터는 전혀 정답을 맞추지 못하는 모델의 상태를 일컫는다.
이전의 포스팅에서 말했듯 과학습의 대책의 하나로 학습 곡선을 그리는 것이 효과적이라고 했는데, 이 포스팅에서 학습곡선에 대해 조금 더 자세히 정리해볼 생각이다.
1. 학습 곡선이란?
학습곡선이(learning curve)란 훈련 데이터의 양에 대해, 모델의 범화성능을 플롯한 것이다. 즉, 훈련 데이터에 대한 모델의 성능과 검증 데이터에 대한 모델의 성능이 훈련 데이터의 양에 따라 어떻게 변화해가는지를 표시한 그래프이다. 다음과 같은 이미지라고 할 수 있다.
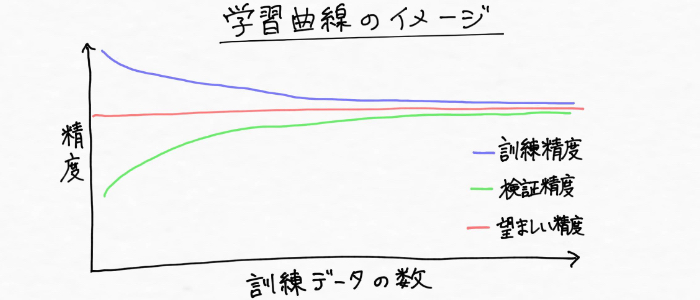
| ※ 플롯 : 관측치 등을 점으로 그래프에 그려 넣는 것 ※ 검증 데이터 : 모델의 성능을 평가하기 위해 사용하는 데이터 |
이 그래프를 보았을 때, 바로 이전의 포스팅에서도 말했듯 훈련 데이터의 양을 무조건 늘리는 것이 모델의 성능을 향상시킬 수 있는 것은 아니라는 사실을 알 수 있다.
2. 학습곡선을 보는 방법
과학습에 빠져있는지, 아님 학습이 부족하여 훈련 데이터 조차 제대로 적합되지 않는 학습 부족(미학습, underfitting)인지를 판단하는 데에 학습 곡선이 중요하다고 하다는 것을 우리는 알고 있다.
참고로, 통계나 머신러닝의 분야에서 위와 같은 상황을 아래와 같이 표현하기도 한다.
|
● 학습부족 = '바이어스(Bias)가 높다(バイアスが高い/ハイバイアス)' ● 과학습 = '바리언스(variance)가 높다 (バリアンスが高い/ハイバリアンス)' |
학습 곡선을 더욱 이해하기 위해, 모델의 바이어스가 높은(학습 부족) 상황과 바리언스가 높은 (과학습) 상황으로 나눠서 학습곡선을 살펴보자.
1) 바이어스가 높은 상황(학습부족)에서의 대책
먼저 '바이어스'는 '편향'이라는 의미를 가진 말이지만, '모델의 바이어스가 높다', '하이바이언스의 상황(학습 부족)'이라는 것은 위 그림과 같이 훈련 데이터의 패턴을 잘 파악하기에는 모델의 복잡도가 불충분 (유연성이 낮은) 상황이다.
또한, 훈련 데이터와 모델의 정밀도의 관계성으로 살펴보자면 다음과 같이 훈련 데이터와 교차검증에 의한 정답률 양쪽 모두 낮아진 상황이다. 그리고 진실(真)의 값에 비해 모델의 예측치의 엇갈림도 크다.
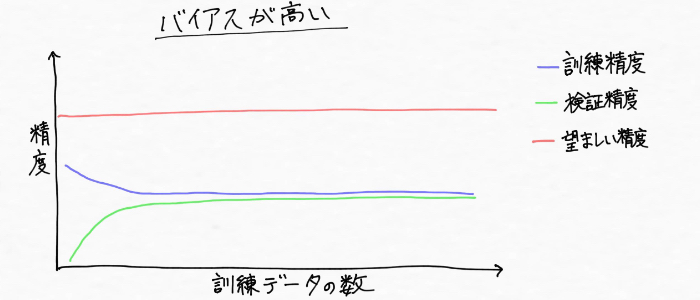
| [Tip] 바이어스가 높은(하이 바이어스) 상황은 예측값이나 측정값이 진실(真)의 값에 어느정도 가까운지를 표시하는 정도를 '정확도'이라 말을 사용하여 '정확도가 낮다'고 말하는 경우도 있다. |
그럼 이와 같이 학습부족(하이 바이어스)에 대한 대책을 살펴보자.
(1) 대책 1 : 머신러닝 알고리즘을 변경한다.
첫 번째 대책은 사용한 머신러닝 알고리즘을 변경하는 것이다. 데이터의 패턴이나 경향을 표현하는 모델은 머신러닝 알고리즘 (머신러닝의 방법)에 의해 구축된다. 사용한 머신러닝 알고리즘에 따라 모델 구축 방법도 달라지기 때문에, 모델의 정밀도가 높아지는지 아닌지는 취급하는 데이터에 따라 바꿔야한다.
즉, 모델이 학습 부족에 빠지면, 원래 사용하고 있던 머신러닝 알고리즘에 문제가 있는지도모른다.
(2) 대책 2 : 모델의 파라미터의 갯수를 증가시킨다.
다음의 학습부족에 대한 대책으로, 머신러닝 알고리즘을 변경하지 않을 경우는 모델의 파라미터의 갯수를 증가(특징량의 수를 증가)시키는 것이 효과적이다.
그러기 위해 예를 들어,
● 추가한 특징량을 수집 혹은 생성한다.
● 모델 정규화의 강도를 낮춘다.
과 같은 것이 필요하다.
※ 정규화 : 과학습을 방지하기 위한 테크닉으로 모델의 형태가 너무 복잡해지지 않도록 제한을 걸어 조정 방법
이와 같은 방법에 의해 모델의 복잡성을 증가시켜 데이터에 보다 적합할 수 있도록 개선할 수 있다. 여기서, 다루지 않고 지나쳤던 '특징량'이라는 말에 대해 잠깐 짚고 넘어가고자 한다.
| [Tips] 특징량 ; 얻고자 하는 것을 특징 짓는 것. 예를 들어, 과거의 판매량으로부터 미래의 판매량을 예측하고 싶은 경우, 날씨와 기온, 습도 등 판매량에 영향을 미치는 정보는 미래의 판매를 예측하기 위해 반드시 필요한 특징량이라고 말한다. |
여기까지의 내용을 정리하자면, 훈련 데이터에 적합하지 않고 진실(真)의 값과의 차이(오차)도 큰 학습 부족의 상황을 바이어스가 높은 (하이 바이어스)라고 표현한다. 사용한 머신러닝 알고리즘을 변경하거나, 모델의 학습에 이용한 특징량을 증가시켜 정규화에 의한 영향이 작아지도록 하는 방법이 효과적이라고 할 수 있다.
2) 하이 바이런스(과학습)에서의 대책
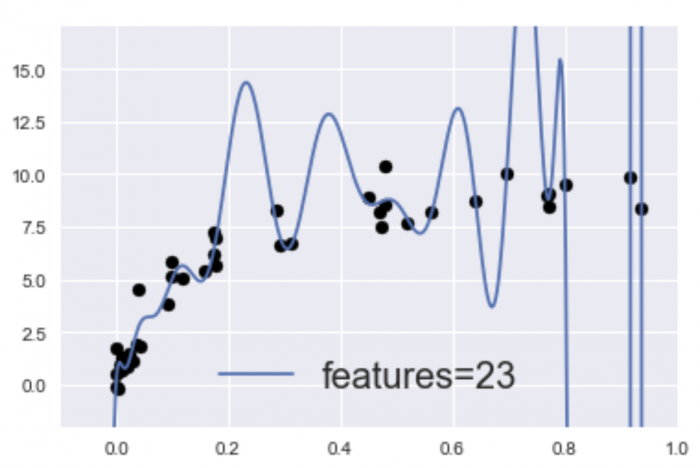
다음은 바이런스가 높은 상황을 살펴보자. 먼저 바이런스란 '편차'라는 의미의 말이지만, 바이런스가 높다, 하이 바이런스의 상황(과학습)은, 위 그림과 같이 훈련 데이터에 대해서는 과도하게 적합하여 높은 성능을 발휘하지만, 검증 데이터(미지의 데이터)에 대해서는 정밀도가 낮은 상황 (범화성능이 없는 상황)이다.
또한 훈련 데이터와 모델 정밀도의 관계성으로 살펴보자면, 다음과 같이 훈련 데이터와 교차검증에 의한 정밀도가 크게 차이 나는 상태이다.
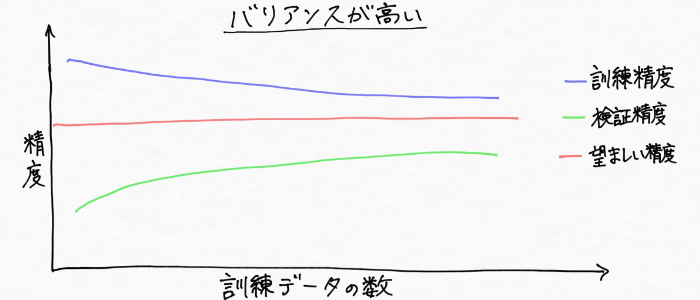
| [Tips] 하이 바리언스는, 예측이나 측정을 여러 번 실시한 경우의 결과의 편차의 크기를 나타내는 정도 '정밀도'라는 표현을 사용해서 '정밀도가 낮다'라는 표현되는 경우가 있다. |
하이바이런스(과학습)의 원인으로는, 파라미터의 수가 너무 많아 데이터에 대한 모델이 너무 복잡해진 것이라고 생각할 수 있다.
사실, 아까 소개한 이 그래프는,

25개의 특징량(features=23)에 적합하도록 지정된 모델을 구축한 것이다. 한편, 학습 부족의 모델로써 전에 소개한 아래의 그래프는,

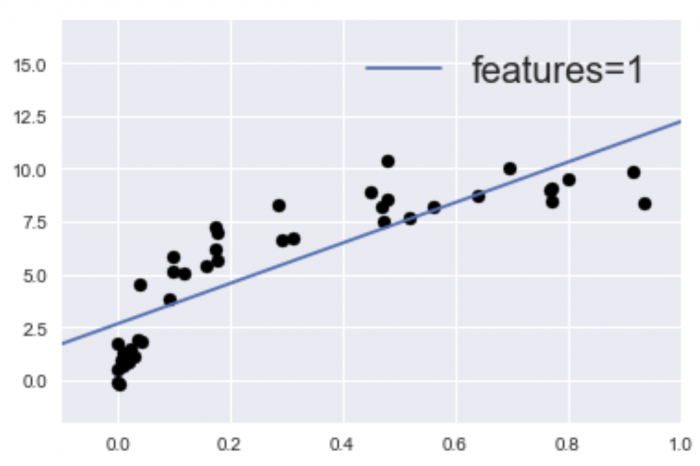
1개(features=1)의 측징량을 적합하도록 지정한 모델을 구축한 것이다.
어찌저찌 모델이 완성되어 버린 하이 바리언스 상태(과학습)의 대책으로는 이전에 살펴봤던, '훈련 데이터의 수를 증가시킨다' '정규화를 실시하여 모델의 복잡성을 억제한다'등이 있다.
머신러닝의 모델에 따라는 정규화가 적용되지 않은 것도 있지만, 그러한 모델의 정밀도를 향상시키기 위해서는 특징량의 갯수를 감소시키는 것이 효과적이다.
※ 통계나 머신러닝의 분야에서 구하고 싶은 것을 '목적 변수', 목적변수를 사용한 변수를 '설명 변수'라고 말하기도 한다.
특정량의 갯수는 '차원'이라고 할 수 있다. 그리고 차원의 감소는 목적 변수에 작용하는 설명 변수(파라미터의 수)를 감소시키는 것으로 예를 들어 특정량의 설명으로 기재되어 있는 미래의 판매량을 예측하는 것을 예로 들자면, 판매량(목적변수)에 작용하는 날씨나 기온, 습도 등(설명 변수)의 중에 하나를 사용하지 않고 모델을 학습시키는 것이다.
즉 정리하자면, 특징량의 갯수 = 차원 = 설명변수의 수라고 할 수 있다.
이와 같이 목적변수에 작용하는 설명변수의 수 (특징량의 갯수, 차원)을 감소하는 것으로, 모델이 적합하도록 하는 요소가 감소되어 형태가 심플해져 하이 바리언스(과학습)을 해소할 수 있다.
여기까지의 내용을 정리하자면, 훈련 데이터와 교차검증의 정밀도에 큰 차이가 있는 과학습의 상황을 바이런스가 높다(하이 바이런스)라고 표현한다. 모델의 학습에 사용하는 특정량을 감소하거나, 정규화에 의한 영향을 강하게 하는 등의 대책이 효과적이다.
3. 범화 성능이 높은 모델 = 바이어스와 바이런스가 적당한 곳을 발견
여기까지는 하이 바이어스(학습부족)과 하이 바이런스(과학습)을 나타내는 학습곡선을 살펴보았지만, 모델의 바람직한 상황을 나타내는 학습곡선은 다음과 같이 훈련 데이터(파란색)에 대해서도 검증 데이터(초록색)에 대해서도 높은 정밀도가 나타난다.
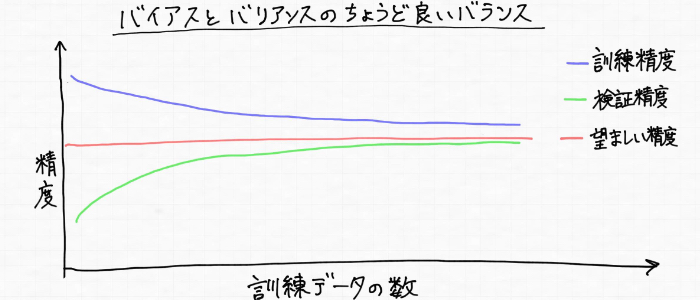
그리고 위의 상황을 모델 형태로 나타내면 다음과 같은 이미지이다.
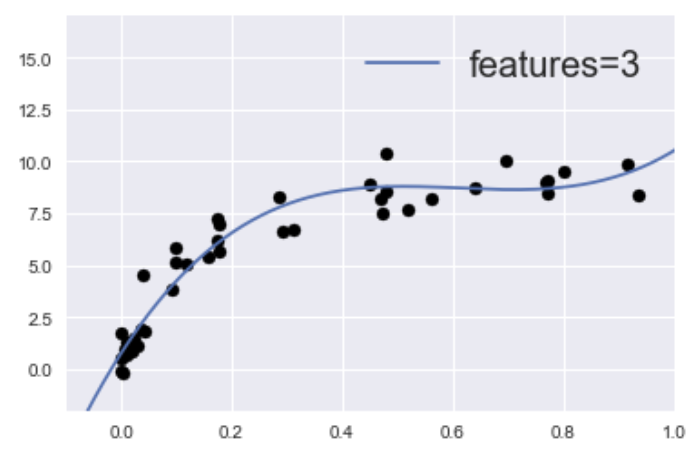
딱딱하지 않고, 부드러운 곡선이 된다. 바이어스가 너무 높아도 안 되고, 바이런스가 너무 높아도 안 된다. 즉 범화 성능이 높은 모델을 얻기 위해서는, 바이어스와 바이런스의 적당한 트레이드 오프(トレードオフ)의 장소를 발견해야하는 것이다.
※ 트레이드 오프(トレードオフ) : 한 쪽을 추구하면 다른 쪽을 희생하지 않으면 안되는 상태, 관계를 일컫는다.
4. Python으로 학습곡선을 그려보자.
유방암 판단 데이터(합계 569명분)가 포함된 데이터 세트가 공개되어 있기 때문에 이번에는 이것을 이용한다. 이것은 종양의 이미지를 바탕으로 종양의 '평균 반경'이나 '바깥쪽의 길이' 등 30개의 측정 항목(특징량)이 각 사람마다 정리되어 있는 데이터 세트이다.
※ 데이터 세트의 중간의 일부를 소개하자면 아래와 같다.↓
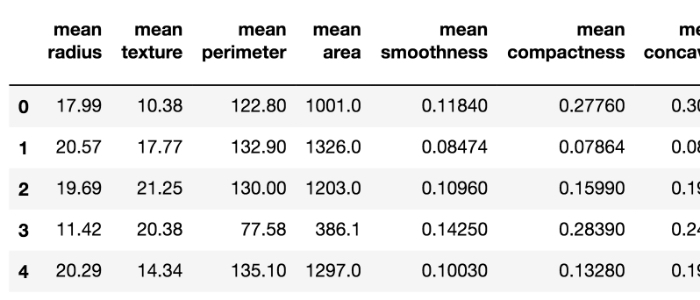
한 행씩 종양의 특징이 정리되어 있다. 30개의 특징량을 모은 569명의 데이터가 있으므로, 569행 x 30행 데이터 세트이다.
이 데이터 세트에 대해서 진단한 종양이 악성인지 음성인지 예측하는 머신러닝 모델을 실제로 구축하여 그 모델의 학습곡선 (learning curve)를 표현하면 아래와 같다.
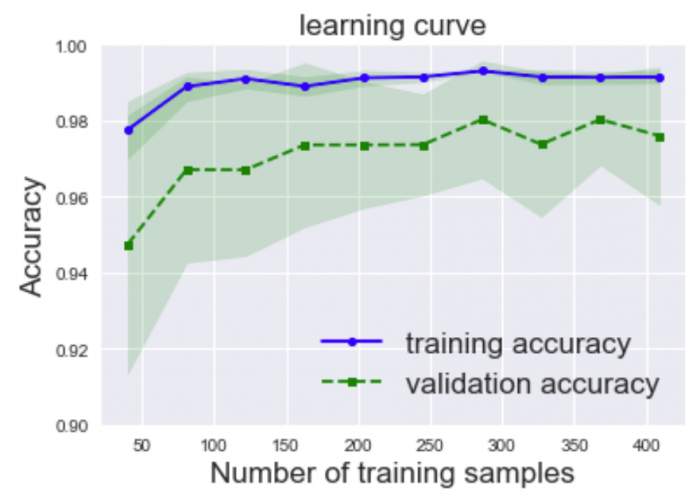
| (보충) · number of training samples : 훈련 데이터의 수 · Accuracy : 모델의 예측에 대한 정답률 · training accuracy : 훈련 데이터에 대한 정답률 · validation accuracy : 검증 데이터에 대한 정답률 띠의 색상은 정답률의 표준편자를 표시한 것으로, 표준편차란 값의 편차를 보는 지표이다. |
학습 곡선을 생성할 때 작성한 코드는 아래와 같다.
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn; seaborn.set()
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.learning_curve import learning_curve
from sklearn.cross_validation import train_test_split
# 데이터 읽어들이기 (データの読み込み)
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',header=None)
# 데이터를 목적 변수와 설명 변수로 나누기(データを目的変数と説明変数に分割する)
X = df.loc[:,2:].values
y = df.loc[:,1].values
# 카테고리별 변수를 연속값으로 변환하기 (カテゴリカル変数を連続直に変換する)
le = LabelEncoder()
y = le.fit_transform(y)
# 훈련 데이터와 테스트 데이터 분할하기 (訓練データとテストデータにデータを分割)
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.20, random_state=1)
# 파이프라인을 이용해 데이터의 스케일 변환을 실시, 로지틱스 회귀를 준비
# (パイプラインを用いてデータのスケール変換を行い、ロジスティック回帰を準備する)
pipe_lr = Pipeline([('scl',StandardScaler()), ('clf',LogisticRegression(penalty='l2',random_state=0))])
# learning_curve함수에서 교차검증에 의한 정답률을 계산한다.
# (learning_curve関数で交差検証による正解率を算出する)
train_sizes, train_scores,test_scores = \
learning_curve(estimator=pipe_lr, X=X_train, y=y_train, train_sizes=np.linspace(0.1,1.0,10), cv=10, n_jobs=1)
train_mean = np.mean(train_scores,axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores,axis=1)
test_std = np.std(test_scores,axis=1)
# 학습곡선을 그린다.
# (学習曲線を描画する)
plt.plot(train_sizes,train_mean, color='blue', marker='o', markersize=5, label='training accuracy')
plt.plot(train_sizes,test_mean, color='green',linestyle='--', marker='s', markersize=5, label='validation accuracy')
# fill_between함수에서 평균±표준편차의 폭을 빈틈없이 칠한다.
# (fill_between関数で平均±標準偏差の幅を塗りつぶす)
# 학습 데이터의 사이즈 train_sizes, 투명도 alpha, 컬러 'blue'를 인수로 지정
# (トレーニングデータのサイズtrain_sizes,透明度alpha、カラー'blue'を引数に指定)
plt.fill_between(train_sizes,train_mean+train_std,train_mean-train_std,alpha=0.15,color='green')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15,color='green')
# 그래프에 한 눈에 정리 (グラフの見た目を整える)
plt.title('learning curve', fontsize=17)
plt.xlabel('Number of training samples', fontsize=17)
plt.ylabel('Accuracy', fontsize=17)
plt.legend(loc='lower right', fontsize=17)
plt.ylim([0.90,1.0])
# 그래프 표시 (グラフを表示)
plt.show()5. 하이퍼 파라미터와 모델의 성능의 변화를 시각적으로 확인할 수 있는 검증 곡선
학습 곡선의 경우는 '훈련 데이터의 양' 과 '모델의 성능'의 관계성을 보는 것이라면, 검증 곡선은 '훈련 데이터의 양'이 아닌 모델의 '하이퍼 파라미터의 값'에 따라 모델의 성능이 어떻게 변화하는지를 확인하는 툴이라고 할 수 있다.
1) 검증곡선을 그려보았다.
앞서 살펴 본 종양을 악성인지 음성인지 분류하는 데이터 세트를 이용하여 검증곡선을 그려보자.
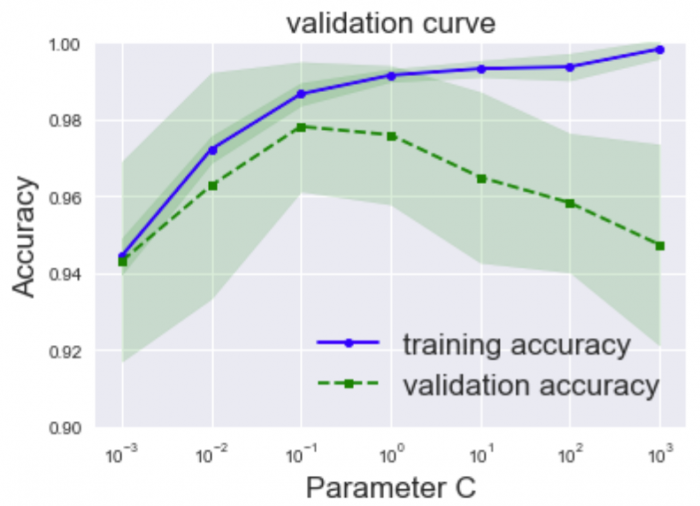
| (보충) · Acuuracy : 모델의 예측에 의한 정답률 · traininig accuracy : 훈련 데이터에 의한 정답률 · validation accuracy : 검증 데이터에 의한 정답률 · ParameterC : 파라미터 C (하이퍼 파라미터) |
위 그래프를 살펴보면 ParameterC의 값이 점점 커지면 훈련 데이터와 검증 데이터의 모델 성능의 차가 점점 벌어져, 즉 과학습에 빠지는 경향으로 끝난다. 적당한 하이퍼 파라미터의 값은 어디라고 할 수 있냐면, 훈련 데이터와 검증 데이터 둘 다 성능이 높은 한편, 양쪽의 성능의 차가 작은 0.1부근에 ParmeterC를 설정하면 좋을 것이라고 판단할 수 있다.
| [Tips] 적당한 하이퍼 파라미터를 조정하는 것을 일반적으로 '파라미터 튜닝'이라고 말한다. |
이와 같이 검증곡선을 확인하는 것으로 최적의 하이퍼 파라미터을 설정할 수 있다.
2) 검증곡선을 생성할 때 사용한 코드
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn; seaborn.set()
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.learning_curve import validation_curve
# 데이터를 읽어들인다. (データの読み込み)
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',header=None)
# 데이터를 목전 변수와 설명 변수로 나눈다. (データを目的変数と説明変数に分割する)
X = df.loc[:,2:].values
y = df.loc[:,1].values
# 카테고리 변수를 연속값으로 변환한다. (カテゴリカル変数を連続直に変換する)
le = LabelEncoder()
y = le.fit_transform(y)
# 훈련 데이터와 테스트 데이터로 나눈다. (訓練データとテストデータにデータを分割)
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.20, random_state=1)
# 파이프 라인을 이용하여 데이터의 스케일 변환을 실시하고, 로지스틱 회귀를 준비한다.
# (パイプラインを用いてデータのスケール変換を行い、ロジスティック回帰を準備する)
pipe_lr = Pipeline([('scl',StandardScaler()), ('clf',LogisticRegression(penalty='l2',random_state=0))])
# 탐색하고 싶은 하이퍼 파라미터를 준비한다. (探索したいハイパーパラメータを準備する)
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
# learning_curve 함수로 교차검증에 의한 정답률을 계산한다.
# (learning_curve関数で交差検証による正解率を算出)
train_scores,test_scores = \
validation_curve(estimator=pipe_lr, X=X_train, y=y_train, param_name='clf__C', param_range=param_range, cv=10)
train_mean = np.mean(train_scores,axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores,axis=1)
test_std = np.std(test_scores,axis=1)
# 학습곡선을 그린다.
# (学習曲線を描画する)
plt.plot(param_range,train_mean, color='blue', marker='o', markersize=5, label='training accuracy')
plt.plot(param_range,test_mean, color='green',linestyle='--', marker='s', markersize=5, label='validation accuracy')
# fill_between함수로 평균±표준편차의 폭을 빈틈없이 칠한다.
# (fill_between関数で平均±標準偏差の幅を塗りつぶす)
#トレーニングデータのサイズtrain_sizes,透明度alpha、カラー'blue'を引数に指定
plt.fill_between(param_range, train_mean + train_std, train_mean - train_std, alpha=0.15,color='green')
plt.fill_between(param_range, test_mean + test_std, test_mean - test_std, alpha=0.15,color='green')
# 그래프를 한 눈에 보기 좋게 정리
# (グラフの見た目を整える)
plt.title('validation curve', fontsize=17)
plt.xscale('log')
plt.legend(loc='lower right', fontsize=17)
plt.xlabel('Parameter C', fontsize=17)
plt.ylabel('Accuracy', fontsize=17)
plt.ylim([0.9,1.0])
# 그래프 표시 (グラフを表示する)
plt.show()여기까지의 내용을 정리하자면, 검증곡선이란 모델의 하이퍼 파라미터의 값에 따라 모델의 성능이 어떻게 변화하는 지를 나타내는 그래프이다. 검증곡선을 보는 것으로 범화성능을 높일 수 있는 적당한 하이퍼 파라미터의 값을 시각적으로 탐색할 수 있다.
3) 적당한 하이퍼 파라미터를 자동적으로 탐색해주는 그리드 서치(グリッドサーチ)
머신러닝 알고리즘에서도 하이퍼 파라미터에서도 다양한 종류가 있으며, 복수의 하이퍼 파라미터를 지정하지 않으면 안 되는 경우도 있다.
적당한 값을 모아 매번 손을 움직여 하나씩 확인하지 않으면 안될까라고 생각할 수 있을 것이다. 그러한 고민을 해결할 수 있는 것이 바로 '그리드 서치'라는 것이다. 그리드 서치란 하이퍼 파리미터의 '적당한' 구성을 발견해줘 모델의 성능을 더욱 개선하는데 도움이 되는 방법이다.
그리드 서치는 다음과 같이 구현할 수 있다.
#グリッドサーチによるハイパーパラメータチューニング
import pandas as pd
from sklearn.svm import SVC
from sklearn.preprocessing import LabelEncoder
from sklearn.cross_validation import train_test_split
from sklearn.model_selection import GridSearchCV
#乳がんの診断データの読み込み
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',header=None)
#データを目的変数と説明変数に分割する
X = df.loc[:,2:].values
y = df.loc[:,1].values
#カテゴリカル変数を連続直に変換する
le = LabelEncoder()
y = le.fit_transform(y)
#訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20,random_state=1)
#探索したいハイパーパラメータの組み合わせを指定する
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
param_grid = {
'C' : param_range,
'gamma' : param_range,
'random_state' : [0, 1, 2, 3, 4, 5]
}
#サポートベクターマシンの最適なハイパーパラメータの組み合わせを10分割交差検証によって探索することを指定
grid_search = GridSearchCV(SVC(), param_grid, cv=10)
#グリッドサーチを用いて最良の性能を出すパラメータを選出し、そのパラメータを用いて訓練データで学習する
grid_search.fit(X_train, y_train)
print(f"テストデータに対するモデルの精度:{grid_search.score(X_test, y_test):.3f}")
print(f"モデルのハイパーパラメータ : {grid_search.best_params_}")
#Out
テストデータに対するモデルの精度:0.956
モデルのハイパーパラメータ : {'C': 1.0, 'gamma': 0.001, 'random_state': 0}최적의 하이퍼 파마리터의 구성(이 경우는 6x6x6 = 216가지 중에서)을 자동적으로 찾아주었다. 여기까지의 내용을 정리해보면 그리드 서치는 하이퍼 파라미터의 값의 적당한 구성을 발견하여 보다 모델의 성능이 좋아지도록 하는 방법으로, 엄청난 많은 구성을 사람 대신에 컴퓨터가 자동적으로 찾아주는 굉장히 편리한 툴이다.
참고자료
'IT > AI\ML' 카테고리의 다른 글
| GAN ; PG-GAN(Progressive Growing of GANs) (0) | 2020.07.06 |
|---|---|
| 머신러닝 분류 모델의 성능평가 (0) | 2020.05.27 |
| 머신러닝 정밀도의 향상을 위해 해야할 것 (0) | 2020.05.24 |
| [python] 교차검증(cross validation/クロスバリデーション/交差検証)과 그 방법들 (0) | 2020.05.19 |
| GAN ; WGAN & WGAN-gp (0) | 2020.05.01 |