1. PG-GAN(Progressive Growing of GANs)의 개요
PG-GAN를 한 마디로 설명하면, '저해상도의 이미지로부터 시작해 네트워크의 레이어를 추가해가며 점차 해상도를 높여가는 GAN'라고 할 수 있다.
기존의 GAN과 같이, 모든 스케일에 대해 동시에 학습하는 것이 아닌, 먼저 처음에 대략 이미지 구성을 파악한 뒤 단계적으로 세부적인 부분에 주목해 간다.

위 그림의 NxN은 해상도가 NxN인 convolution층을 의미한다. 참고로 모든 층은 항상 훈련이 가능한 상태이다.
본 연구의 학습에서는 Generator과 Discriminator 각각 저해상도 (4x4)의 층으로 부터 시작하여 학습이 진행해감에 따라 조금씩 Generator과 Discriminator에 층을 추가해나가는 것으로 생성 이미지의 해상도를 향상시킨다.
이 방법을 통해 고해상도의 이미지를 생성이 안정화되고, 학습시간의 단축이 가능하게 되었다.
위 그림의 오른쪽 이미지 6장은 방금 언급한 단계적인 학습법 (해상도: 1024 x 1024)에 의해 생성된 이미지이다.

Generator과 Discriminator의 해상도를 2배로 증가시킬 때, 새로운 층을 넣는다.
16x16의 해상도로부터 32x32의 해상도로의 변화를 나타내고 있다. (위 그림의 (a)부터 (c) 그림의 변화)
이러한 변화 과정을 나타낸 그림이 위 그림의 (b)이다.
고해상도의 층에서는 잔차(残差)블록처럼 되어 있다. 그림의 각 요소에 대해서 설명하자면,
- α는0~1 사이의 값
- 2 X 과 0.5 X는 각각 해상도를 2배, 0.5배로 하는 것
- toRGB는 특징 벡터를 RGB에 변환하는 층, fromRGB는 그 반대이다. 어느 쪽도 1x1의 Convolution층을 사용
을 의미한다.
Disciriminator을 훈련할 때는 현재의 네티워크의 해상도에 맞게 축소된 진짜의 이미지를 입력한다.
잔차(残差)블록을 사용하고 있으므로, Generator의 출력은 2개의 이미지(to RGB된 것)을 더하면 마찬가지로 Discriminator에서는 2개의 벡터(from RGB된 것)
2. 네트워크 구성

위 그림의 왼쪽은 Generator의 아키텍처이고 오른쪽은 Discriminator의 아키텍처이다. 둘 다 3층을 하나의 블록으로 한 것을 학습 도중에 1개씩 늘려 가며 쌓아갔다는 것을 알 수 있다.
Generator의 최후의 1x1의 Convolution층은 toRGB를 의미하고, Discriminator의 최초의 1x1의 Convolution층은 fromRGB를 의미한다.
업샘플링은 2x2로 복제, 다운샘플링은 평균풀링한다.
잠재벡터는 512차원으로 실제 이미지와 생성 이미지는 [-1, 1]의 범위로 표시한다.
leaky ReLU(α=0.2)를 선형변환하는 마지막 층을 제외하고, 두 네트워크의 모든 층을 사용한다.
1) 학습의 흐름
4x4의 해상도로부터 시작해, Discriminator에 합계 800장의 진짜 이미지를 보여줄 때까지 네트워크 학습을 실시한다. 그 후에는 다음의 2개의 처리를 반복해서 실행한다. (① → ② → ① → ....)
① 새로운 3층짜리 블록을 넣는다 (해상도를 향상시킴)
② 800장의 진짜 이미지로 네트워크를 안정화시킨다.
2) 아이디어 (후술)
batch normalization・layer normalization・weight normalization는 어느쪽의 네트워크에도 사용하지만, Generator의 3x3의 Convolution층의 후에 pixelwise normalization (후술: Generator에 있어 픽셀 특징 벡터의 정규화)를 사용한다.
바이어스는 0으로 초기화하고, 가중치는 분산 1의 정규 분산에 따른다. 그러나, 학습할 때 각 층 고유의 정수로 가중치를 스케일링한다. (후술 : 학습률의 균질화)
Descriminator의 마지막 층은 4x4의 해상도로 미니배치 전체의 표준편차의 특징 맵을 추가한다. (후술: 미니배치 표준편차를 사용한 이미지는 다양성을 향상시킨다.)
3) 최적화 함수
Adam (α=0.001, β1=0, β2=0.99, ε=10의 -8승)
4) 미니배치사이즈
해상도 ( 4 x 4 ~ 128x128) : 미니배치사이즈 = 16
해상도 (256 x 256) : 미니배치사이즈 = 14
해상도 (512 x 512) : 미니배치사이즈 = 6
해상도 (1024 x 1024) : 미니배치사이즈 = 3
미니배치사이를 점점 작게 하는 것은 메모리에 적재하기 위함이다.
3. PGGAN의 장점
1) 학습의 안정화
맨 처음은 작은 굉장히 작은 이미지이므로 대폭 안정화하여 생성할 수 있다.
▶ 이유 : 클래스 정보, 모드 정보가 적다.
해상도를 조금씩 향상시켜가는 것에 따라 단순한 질문에 대답하는 것과 같은 상황으로 학습이 진행된다.
기존의 GAN의 경우, 잠재표현부터 1024 x 1024의 이미지로의 맵핑이라는 어려운 최종목표를 달성할 수 있도록 시행착오를 거칠 수 밖에 없다. 복잡한 잠재표현으로부터 고해상도의 이미지로의 맵핑은 단계적으로 배우는 것이 간단하다.
(PGGAN의 경우) 하나의 층을 넣어 충분히 학습한다. → 새로운 층 (해상도가 전보다 높은 층)을 넣는다. → 충분히 학습한다. → ...
하나의 층을 제대로 학습해 안정화한 후에 다음 층을 넣는 정중한 방법이며, 기존의 GAN의 경우 처음부터 모든 층을 넣어 단번에 모든 층을 학습한다. 즉, PGGAN에 비해 복잡한 방법이다.
수학을 배우는 것을 예시로 들어 보자면, PGGAN의 경우 덧셈을 학습한다. → 뺄셈을 학습한다. → 곱셈을 학습한다. → .... → 센터시험의 수학과 같은 단계를 거치면, 기존의 GAN은 첫 날에 바로 센터 시험의 수학 공부를 하는 것이다.
실제로는 WGAN-GP 손실이나 LSGAN손실을 사용하여, 메가 픽셀 스케일의 이미지를 확실히 생성하기 위한 학습을 충분히 안정화시킨다.
2) 학습시간의 단축
PGGAN에서는 대부분의 이터레이션(반복)이 저해상도에서 실행되므로 (물론 최종적으로 출력되는 해상도에 따라 다르겠지만) 기존의 GAN보다 2~6배 빠르게 학습이 가능하다.
4. 미니배치 표준편차를 사용한 이미지 다양성의 향상
GAN는 훈련 데이터 일부 이미지의 특징이나 패턴만을 파악하는 경향이 있으므로 해결책으로써 '미니배치 식별'이 제안되었다.
이것은 각각의 이미지뿐만 아니라 미니배치 전체로부터도 특징통계량을 계산하는 것이다. 최종적으로는 생성 이미지의 미니배치와 훈련 이미지의 미니배치라 같은 통계량을 표시하는 것이 이상적이다.
미니배치층은 Discriminator의 마지막에 추가하는 것으로 구현할 수 있다. 미니배치층에는 입력 활성화를 통계량에 변환하는 텐서를 학습한다.
미니배치 각 샘플로부터 생성된 다양한 통계량이 층의 출력과 합쳐지므로 Disicriminator은 통계량을 사용하는 것이 가능하다. 본 연구에서는 이런 처리를 대폭 단순화하여 이미지의 다양성도 향상시켰다.
1) 심플한 버전

본 연구에서는 단순화시킨 방법은 학습 가능한 파라미터나 새로운 하이퍼 파라미터를 사용할 뿐만 아니라
① 미니배치 상의 각 공간위치에 있어 각 특징의 표준편차를 계산한다.
② 모든 특징, 모든 공간에서 평균을 계산하여 단 하나의 값을 출력한다.
③ 그 값을 복제하여 1장의 특징맵을 만든다.
이 층은 어디서든 삽입하는 것이 가능하지만, 마지막층에 입력하는 것이 제일 좋다는 것을 알 수 있다.
5. Generator과 Discriminator의 정규화
GAN에서는 Generator과 Discriminator의 학습에 따라 값의 발산이 일어나기 쉽다. 이러한 문제를 해결위한 대책으로 2가지 방법이 제안된다.
1) 학습률의 균질화
초기값은 N(0,1)으로 하여, 학습할 때 가중치를 동적으로 스케일링한다. 가중치를 스케줄링하는 데에는 아래의 식을 사용한다.

wi는 가중치, c는 각층의 정구화 정수(He의 초기화를 사용한다.) → 스케일 불변성을 얻을 수 있다.
최적화할 때 스케일의 영향을 받지 않고 파라미터의 갱신이 가능하도록 하기 위해 학습 속도가 올라간다. 스케일을 갖추고 있기 때문에 모든 가중치에 대해 균질의 학습 속도로 가능하다.
2) Generator에 있어 픽셀 특징 벡터의 정규화
Generator의 각 convolution층에의 통계후에 각 픽셀의 특징 벡터를 정규화한다. 정규화는 아래의 식을 따른다.

ε=10의−8승, N= 특징 맵의 수, ax,y = 픽셀(x, y)의 정규화전의 특징 벡터, bx,y = 픽셀(x, y)의 정규화한 특징 벡터
6. GAN평가를 위한 멀티 스케일의 통계적 유사성
잘 학습된 Generator은 국소적인 이미지 구성이 모든 스케일에 걸쳐 진짜 이미와 비슷한 이미지를 생성한다.
16x16픽셀의 로우 패스 해상도로부터 시작해, 생성 이미지의 라플라시안 피라미드 표현에 의한 국소 이미지의 분산과 가짜 이미지의 라플라시안 피라미드 표현에 의한 국소 이미지의 분산의 멀티 스케일 통계적 유사성에 대해서 생각해보자.
짧게 말하자면, 멀티 스케일로 생성 이미지와 가짜 이미의 분산을 비교하여, 분산의 거리가 가까울수록 좋은 GAN라고 생각된다.
※ 라플라시안 피라미드에 대해서는 "laplacian pyramid"에서 이미지 검색하면 어떤 이미지인지 알 수 있을 것이다.
1) 국소 특징량을 얻는다.
지금까지의 관례에 따라, 피라미드는 full 해상도에 도달하기 까지 단계적으로 2배로 한다. 각 레벨은 그 전의 레벨을 업샘플링한 것과의 차이를 인코딩한다.
라플라시안 피라미드의 각 레벨은 특징의 공간주파수대역에 대응한다. 랜덤으로 16384장의 이미지를 선택해, 각 이미지의 라플라시안 피라미드의 각 레벨로부터 128개 국소 특징량을 추출한다.
그러면 각 레벨로부터 2의 21제곱(2.1M)개의 국소 특징량을 얻을 수 있다. (16384 x 128 = 2의 21제곱)
각각의 국소 특징량은 7x7의 픽셀의 3채널 x∈R의147 제곱으로 표시한다. 훈련 데이터의 레벨 l로부터의 국소 특징량은 아래와 같이 표시,

생성 데이터의 레벨 l로부터의 국소 특징량은 아래와 같이 표시한다.

2) 분산거리를 예측한다.
① 각 채널의 평균과 표준차를 구하여 훈련 데이터의 국소 특징량과 생성 데이터의 국소 특징량의 정규화를 실행한다.


② x와 y의 통계적인 유사성을 sliced Wasserstrin distance(SWD)
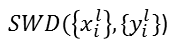
로 계산한다. Wasserstein distance거리는 수송 문제에 따라 고려된 분산의 거리를 예측하는 지표이다. Wasserstein distance거리가 작다는 것은 분산이 유사하다는 것,즉 이 해상도에의 훈련 이미지와 생성이미지는 외형도 다양성도똑같이보인다는것을의미한다.
최저해상도의 16x16의 분산 거리는 대략적인 이미지 구성의 유사성을 표시해, 고해상도에의 분산 거리는 선이나 노이즈의 선명도 등 픽셀 수준에의 정보의 유사성을 나타낸다.
7. 검증
1) 학습구성을 바꾼 결과는 어떻게 됐을까?
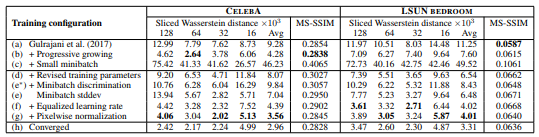

위 표는 다양한 학습 구성에서의 SWD(Sliced Wasserstein distance)과 MS-SSIM(multi-scale structural similarity)의 수치 평가를 표시한 것이다.
2) 위 표를 볼 때의 주의점
일반적으로 평가 지표의 수치가 좋은 것은 색, 텍스처 등의 다양성이 있는 것을 의미하지만, MS-SSIM을 볼 때는 주의가 필요하다. 위 그림을 보면 (a)보다는 (h)가 명확히 깔끔한 이미지가 된 것이 MS-SSIM의 수치가 거의 같다.
이것은 MS-SSIM이라는 지표는 생성 이미지의 다양성만을 평가하는 지표이고, 가짜 이미지와의 유사성을 평가하는 것은 아니다. 한편, SVD의 수치는 크게 개선되고 있다.
3) 결과
최초의 학습 구성 (a)는 Gulrajani et al.(2017)이다.
그것은 Generator에 batch normalization을 , Discriminator에 layer normalization을 넣어 미니 배치를 64로 한 경우
(b)는 단계적으로 학습 (층을 점점 증가시켜가며 학습)의 네트워크는 선명한 이미지를 생성하고 있다. 생성 이미지의 분산과 실제 이미지의 분산보다 비슷한 것을 SWD의 수치를 표시하고 있다.
고해상도의 이미지를 생성하는 것이 목표인가, 그것을 위하여 미니배치를 작은 사이즈(메모리에 적재하는 사이즈) 로 할 필요가 있다. 그러한 것을 구현한 것이 (c)이다. 미니배치사이즈를 64로부터 16에 변환하고 있다. 두 지표로부터 알 수 있지만, 생성 이미지는 불명확하다.
batch normalization과 layer normalization를 제거, 하이퍼 파라미터의 조정을 하여 학습 과정을 안정화한 것이 (d)이다. (e*)은 미니배치 식별을 가능하도록 한 것 (Salimans et al., 2016) 이지만, 생성이미지의 다양성을 평가하는 MS-SSIM의 지표조차도 향상하지 못한 결과로 끝나버렸다.
대조적으로 본 연구에서의 미니매치 식별 (e)에서는 SWD의 평균 스코어를 개선하여 선명한 이미지의 생성에도 성공하고 있다. 더욱이 본 연구에서 제안한 (f)과 (g)를 더하면 SWD의 스코어와 생성 이미지의 질이 더욱 좋아졌다.
마지막으로 (h)는 베스트 네트워크를 이용하여 충분한 학습을 한 결과이다. 지금까지의 GAN모델보다도 선명한 이미지를 생성할 수 있었다.
8. 수렴과 학습 시간

위 그림(a)와 (b)는 훈련 시간(가로 축)과 SWD의 수치 (세로 축), 그림 (c)는 훈련 시간(가로 축)과 Discriminator에게 보여준 진짜 이미지의 숫자(세로 축)이다.
(a)와 (b)는 Gulrajani et al. (2017)의 학습 구성에서의 결과이다. 그러나 (a)는 단계적으로 학습 (층을 서서히 추가시켜가며 학습)의 네트워크가 아니며 (제일 처음부터 모든 층을 네트워크에 넣어 둔 것), (b)는 단계적 학습 (층을 서서히 추가시켜 학습)의 네트워크이다.
단계적인 학습은 2개의 메리트가 있다는 것을 알고 있다.
- 매우 우수한 최적치에 수렴한다.
- 학습 시간을 반으로 줄이는 것이 가능하다.
1) 수렴
수렴성의 향상은 점차 네트워크를 크게 하는 '커리큘럼 학습'에 의한 것이다. 단계적인 학습을 하지 않는 경우는 Generator과 Discriminator의 모든 층은 대략적인 이미지 구성의 다양성과 이미지의 선명도, 두 개의 중간 표현을 동시에 찾아내지 않으면 안 된다. 그러나 단계적인 학습을 할 경우에 처음부터 있었던 저해상도의 층은 이미 빠른 시간에 수렴하므로 새로운 층을 더해서 네트워크는 선명한 표현을 학습하는 것에 전념할 수 있다.
위 그림의 (b) 저해상도인 16x16 (빨간선)이 매우 빠르게 최적한 값을 달성하여, 남은 학습에서는 제자리 걸음을 하고 있는 것을 볼 수 있으며 이는 PGGAN의 학습법의 메리트를 실감할 수 있을 것이다.
저해상도의 층으로부터 순서대로 (16, 32, 64,128)로 수렴하고 있다는 것을 알 수 있다.
2) 학습 시간
세로축은 Discriminator에 보여준 진짜 이미지의 숫자이다. Discriminator에 많은 진짜 이미지를 보여줬다는 것은 그만큼 학습이 진행되었다는 것을 의미한다.
단계적 학습에서는 초기의 학습이 매우 빠른 것을 알 수 있다. 이것은 초기 단계의 네트워크는 계층이 적이 때문에 평가가 빠르게 진행되기 때문이다. full 해상도를 달성하면, Discriminator에 보여준 실제 이미지의 숫자 (학습속도)는 어떠한 방법도 결국 같게 된다.
위 그림은 PGGAN에서는 96시간에 약 640만장의 실제 이미지를 보여준 것을 나타내고 있다. PGGAN가 아니라면 같은 이미지 숫자를 보기위해서는 520시간이 필요하다는 것을 추정할 수 있다. 이 경우 PGGAN는 약 5.4배, 기존보다 빠르다는 것을 알 수 있다.
참고자료
https://www.nogawanogawa.com/entry/pggan
https://curt-park.github.io/2018-05-09/pggan/
https://qiita.com/Phoeboooo/items/ea0e44733e2d2240879b
'IT > AI\ML' 카테고리의 다른 글
| [수학/분포] 정규분포 간의 KL 발산(쿨백-라이블러 발산 ; Kullback–Leibler divergence, KLD) (0) | 2020.08.07 |
|---|---|
| [수학/분포] 확률변수 Jensen 부등식의 직감적 이해 (0) | 2020.08.06 |
| 머신러닝 분류 모델의 성능평가 (0) | 2020.05.27 |
| [python] 머신러닝의 모델 정밀도 향상에 효과적인 학습곡선과 검증곡선 입문 (0) | 2020.05.25 |
| 머신러닝 정밀도의 향상을 위해 해야할 것 (0) | 2020.05.24 |