이번 포스팅에서는 WGAN 및 WGAN의 개선판(WGAN-gp)에 대해서 설명한다.
1. GAN의 문제점
- 학습이 어렵다.
▶ 기울기 손실 문제가 발생한다.
- 생성 결과의 퀄리티를 손실함수로부터 판단하기 힘들다.
- 모드 붕괴가 일어난다.
2. 개선 방법
- Wasserstein GAN의 도입
▶ Wasserstein거리에 의한 손실함수의 설계
▷ 요소를 만족하기 위해 가중치를 클리핑 (WGAN)
▷ 학습이 불안정한 문제
▶ 다른 방법으로는 Grgdient penality를 도입 (WGAN-gp)
3. 기본 구조와 비교하여 변경된 점
|
- 손실함수 (binary cross entropy에서 Wasserstein loss로) - discriminator의 구조 |
(1) 손실함수
먼저 손실함수에 대해 설명한다. 보통의 GAN은 아래의 가치함수의 최적화를 한다.

Discriminator의 최적화시, 우변을 최대화시키는 것이 좋다는 것을 알고 있으므로, 우변 제 1항목이 가급적으로 커지도록 진짜 데이터 (labe=1)에 대해 식별 결과를 진품(1)을 반환하고, 가짜 데이터(0)은 가품(0)을 반환하도록 하는 것이 좋다는 것을 알 수 있다. 결과적으로 이에 대응하는 것이 binary cross 함수라는 것을 설명했었다.
또한, 실제 데이터의 확률밀도분포 Pdata(x)와 생성 데이터의 확률밀포분호Pg(z)가 고정되어 있는 경우, 최적의 식별함수 D*는 아래와 같다.


이 식은 Pdata(x)의 주변(즉 Pg(x)가 거의 0의 구역)에서는, D* = 1로, 역으로 Pg(x)의 주변에서는 D*=0으로 된다. 두 가지의 분포의 교차에서는 D* = 0.5가 된다.
(2) Jensen - Shannon 발산
더욱이 최적한 Discriminator하에서의 Generator의 가치함수는 아래의 식으로 표현할 수 있다.

JSD는 Jensen-Shannon Divergence라는 두 개의 확률 밀도간의 거리를 나타내는 함수이다. JSD가 0이 될 때는, Pdata(x)와 Pz(x)가 (전부 x로) 완전히 일치할 때이다. 바꿔 말하자면 보통의 GAN은 Jensen-Shannon발산을 지표로, 두 개의 확률 밀접도 간의 거리를 학습하여 가까워지도록 작업한다고 간주할 수 있다.
Jesen-Shannon발산을 이용하는 것의 단점은 기울기 손실문제이다. Generator의 파라미터 θ의 최적 값 주변에서 기울이가 0이 되어버려, 학습이 제대로 진행되지 않는다는 사실은 WGAN의 논문에서 지적되어 있다.
여기서 Jensen-Shannon발산의 대신에 다른 지표 (거리)를 이용하여 GAN을 만들고자 한다면 어떤 아이디어가 있을까? 확률분포간의 거리는 여러가지 있지만, Wasserstenin거리를 이용한 컨셉이 Wasserstein GAN(WGAN)이다.
이 거리를 이용하는 메리트는 파라미터의 최적 점 부근에서 기울기가 소실되지 않고, 안습이 안정적으로 진행되는 점이다.
WGAN에서는 Jensen-Shanon 발산의 대신에 Wasserstein거리를 이용한 손실함수를 정의한다. 여러 설명을 날려 버렸지만, 두 가지의 확률밀도간의 Wasserstein거리 w를 아래와 같이 나타낼 수 있다.

keras의 프레임워크에서는 손실함수의 최소화하기 때문에, 위의 식에 마이너스를 걸어서 최소화문제를 정의화하였다. 그 결과 최소화해야할 손실함수 L은 아래의 식이 된다.

x위의 ~이 있는 기호(명칭을 모르겠음) 는 z에서 생성한 이미지를, x는 진짜 이미지를 나타낸다. JSD를 이용한 보통의 GAN에 대해 Wasserstein거리의 특징은 손실함수에 log를 이용하지 않는 것이다. 더욱이 D(x)는 더이상, 식별 결과로써의 의미가 아니므로 출력을 sigmoid함수에 의해 [0,1]로 입력될 필요도 없다. WGAN에서는 D(x)를 f(x)과 표시하거나, Discriminator의 대신에 Critic이라부르거나 한다.
(3) Discriminator의 제약 조건
그런데, D(x)가 Wasserstein거리로써 의미를 가지기 위해서는, 하나의 제약조건이 있다. 그것은 D(x)가 Lipschitz함수인 것이다. 이 부분에 대해서는 더 이상 잘 해석하지 못하겠지만, 제일 초음에 제안된 WGAN에서는 이 제약조건을 충족시키기 위해서 가중치 파라미터를 최소, 최대값을 clip하고 있다.
그러나, 이러한 clip이라는 작업도 상당히 힘을 이용하는 작업같아서 학습이 불안정해질 것 같은 느낌이 든다. 여기서 개선형의 WGAN는, 파라미터의 clip 대신에 critic의 gradient norm손실함수에 패널티 항목을 전달하는 것으로 학습의 최적화를 달성하고 있다.
아래에서 낙하산식이지만 설명하겠다. 최적화된 Discriminator에 있어서 생성 데이터와 진짜 데이터간의 임의의 점에 Discriminator의 생성 데이터 및 진짜 데이터간의 임의의 점 x햇에 대한 기울기의 L2법칙이 1이 되도록하는 성질이 있는듯하다. 이러한 성질을 역이용하여 손실 함수에 기울기의 L2법칙이 1이외의 값일 때, 패널티를 부과하는 것으로, Discriminator의 최적화를 실시한다. 즉 이하의 손실 함수를 최소화하는 개량형 WGAN, 즉 WGAN-gp(gredient penalty)과 동일하다.

여기서, x햇(^)은 생성 데이터와 진짜 데이터를 연결한 직선상의 임의의 점이다.
(4) Discriminator의 구조
WGAN-GP 생성자(generator)는 WGAN 생성자와 같은 방식으로 정의하고 컴파일한다. WGAN와 차이점이 있는 점은 Discriminator부분이다. WGAN의 비평자(discriminator)를 WGAN-gp의 비평자로 정의, 컴파일하기 위해서는 기존의 WGAN비평자에서 세 가지를 바꾸어야 한다.
- 비평자 손실 함수에 그레디언트 패널티 항을 포함한다. 비평자의 가중치를 클리핑하는 대신 비평자의 그레이디언트 노름이 1에서 크게 벗어날 때 모델에 패널티를 부과하는 항을 손실 함수에 포함하는 방식이다.
- 비평자의 가중치를 클리핑하지 않는다.
- 비평자에 배치 정규화 층을 사용하지 않는다.
먼저 보통의 GAN의 Discriminator의 구조는 아래와 같다.
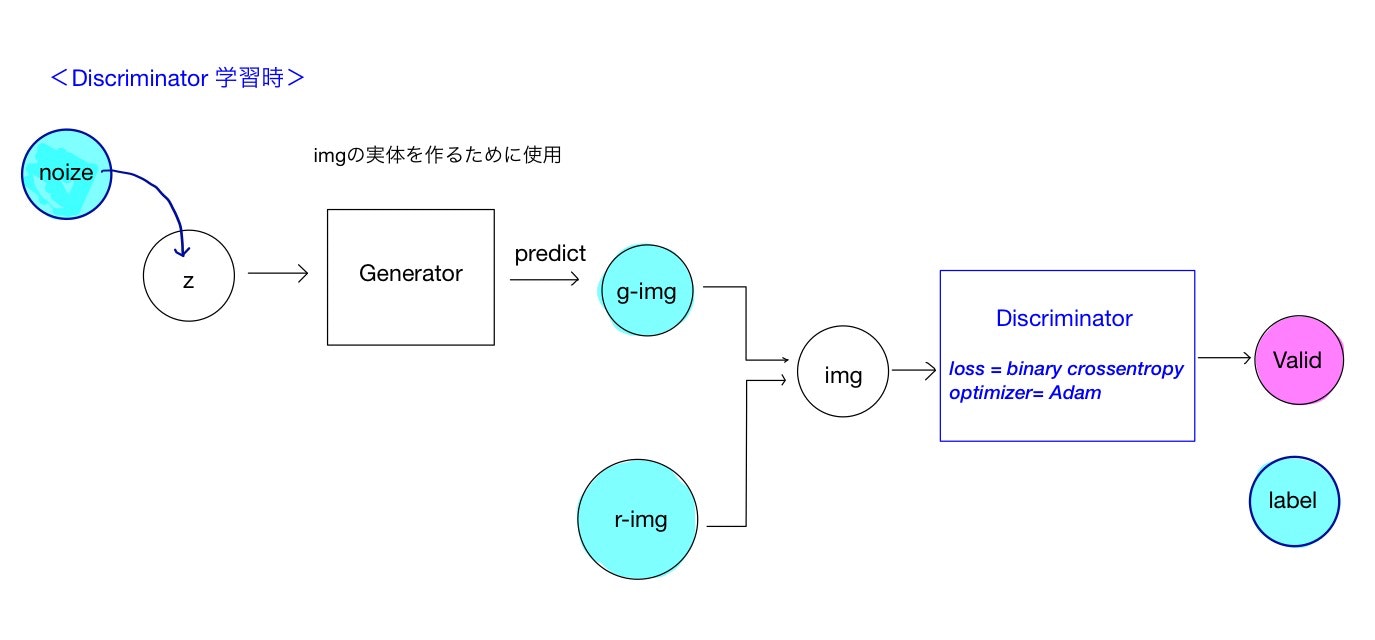
Generator과 Discriminator을 완전히 분리하여, Discriminator만을 고려하였다. 진짜 데이터와 생성(가짜) 데이터를 각각 학습시킨다.
다음은, WGAN-gp의 Discriminator의 구조를 나타내면 아래와 같다.

WGAN-gp에서는 진짜 데이터와 생성 데이터를 동시에 학습시킬 필요가 있으므로, Generator은 분리시키지 않고, 입력데이터로써, 노이즈와 r-img를 이용하는 구조이다. 그러나, Discriminator에 대한 실질적인 입력에 의해 생성된 데이터 f-img (f는 fake의 의미)와 r-img(r은 real의 의미)을 더해, 두 개의 샘플 간의 임의의 점인 a-img(a는 average의 의미)를 이용한다. 두 개의 입력값으로부터 각 입력을 직선으로 연결한 임의의 점을 이용한다(진짜 이미지와 가짜 이미지 쌍을 연결한 직선을 따라 무작위로 포인트를 선택해 보간intrpolation 한 이미지들을 사용한다). 그러기 위한 함수로써 케라스에서는 내장된 _Merge층을 상속한 RandomWeightedAverage층을 만들어 보간 연산을 구현한다.
Discriminator로부터의 출력도 세 가지이다. f-out과 r-out을 이용한 Original critic loss를, a-out를 이용하여 gradient penalty를 기록하여, 손실함수를 정의한다. 최종적으로 Optimizer를 정의하는 것으로 Discriminator의 학습을 진행한다.
# 랜덤한 보간을 수행하는 층
class RandomWeightedAverage(_Merge):
def __init__(self, batch_size):
super().__init__()
self.batch_size = batch_size
def _merge_function(self, inputs):
# 배치에 있는 각 이미지는 0과 1 사이의 랜덤한 수치를 얻어 alpha 벡터에 저장된다.
alpha = K.random_uniform((self.batch_size, 1, 1, 1))
# 이 층은 진짜 이미지(inputs[0])와 가짜 이미지(inputs[1]) 쌍을 연결하는 직선 위에 놓인 픽셀 기준의 보간된 이미지를 반환한다. 각 쌍의 가중치는 alpha 값으로 결정한다.
return (alpha * inputs[0]) + ((1 - alpha)*inputs[1])
아래의 gradient_penalty_loss함수는 보간된 포인트에서 계산한 그레이디언트와 1사이의 차이를 제곱하여 반환한다.
def gradient_penalty_loss(y_true, y_pred, interpolated_samples):
# 케라스의 gradients 함수는 보간된 이미지 입력(interpolated_samples)에 대한 예측(y_pred)의 그레디언트를 계산한다.
gradients = K.gradients(y_pred, interpolated_smaples)[0]
# 이 벡터의 L2 노름(즉, 유클리드Euclidean거리)을 계산하나.
gradinet_l2_norm = K.sqrt(
K.sum(
K.square(gradients),
axis = [1:len(gradients.shape)]
)
)
)
gradient_penalty = K.square(1 - gradient_l2_norm)
# 이 함수는 이 L2노름과 1 사이 거리의 제곱을 반환한다.
reutnr K.mean(gradient_penalty)
두 이미지 사이를 보간할 수 있는 RandomWeightedAverage 층과 보간된 이미지를 위해 그레이디언트 손실을 계산할 수 있는 gradient_penalty_loss 함수가 준비되었다. 이 둘을 사용해 비평자의 모델 컴파일 단계를 수행한다.
WGAN에서는 주어진 이미지가 진짜인지 가짜인지 예측하기 위해 비평자를 직접 컴파일했지만, WGAN-GP비평자를 컴파일하려면 손실 함수에 보간된 이미지를 사용해야 한다. 하지만 케라스는 사용자 정의 손실 함수에 예측과 진짜 레이블 두 개의 매개변수만 허용한다. 이 이슈를 해결하기 위해 파이썬의 partial함수를 사용하였다.
from functools import partial
## 비평자 모델 컴파일
'''
생성자의 가중치를 동결한다.
보간된 이미지가 손실 함수에 관여하기 때문에 생성자는 비평자를 훈련하기 위해 사용할 모델의 일부를 구성한다.
따라서 가중치를 동결해야한다.
'''
self.generator.trainalbe = False
'''
모델의 입력은 두 개이다.
하나는 진짜 이미지의 배치이고 또 하나는 가짜 이미지 배치를 생성하는 데 사용할 랜덤하게 생성한 숫자 배열이다.
'''
real_img = Input(shape=self.input_dim)
z_disc = Input(shape=(self.z_dims,))
fake_img = self.generator(z_disc)
'''
와서스테인 손실을 계산하기 위해 진짜 이미지와 가짜 이미지를 비평자에 통과시킨다.
'''
fake = self.critic(fake_img)
valid = self.critic(real_img)
'''
RandomWeightedAverage층이 보간된 이미지를 만들고 다시 비평자에 통과시킨다.
'''
interpolated_img = RandomWeightedAverage(self.batch_size)([real_img, fake_img])
validity_interpolated = self.critic(interpolated_img)
'''
케라스의 손실 함수는 예측과 진짜 레이블 두 개의 입력만 기대한다.
따라서 파이썬의 partial 함수를 사용해 보간된 이미지를 gradient_penalty_loss함수에 적용한
사용자 정의 함수 partial_gp_loss를 정의한다.
'''
partial_gp_loss = partial(self.gradient_penalty_loss, interpolated_samples = interpolated_img)
partial_gp_loss.__name__ = 'gradient_penalty' # 케라스는 함수 이름이 필요하다.
'''
비평자를 훈련하기 위한 모델에 두 개의 입력이 정의된다.
하나는 진짜 이미지의 배치이고 또 하나는 가짜 이미지를 생성하는 랜덤한 입력이다.
이 모델은 출력이 세 가지이다.
진짜 이미지는 1, 가짜 이미지는 -1, 더미(dummy) 0 벡터이다.
0벡터는 케라스의 모든 손실 함수가 반드시 출력에 매핑되어야 하기 때문에 필요하지만 실제로 사용되지는 않는다.
따라서 partial_gp_loss 함수에 매핑되는 더미 0 을 만든다.
'''
self.critic_model = Model(inputs = [real_img, z_disc], outputs = [valid, fake, validity_interpolated])
'''
진짜 이미지와 가짜 이미지에 대한 두 개의 와서스테인 손실가 그레디언트 페널티 손실 총 세 개의 손실 함수로 비평자를 컴파일한다.
전체 손실은 이 세 가지 손실의 합이다.
원본 논문의 권고 사항에 따라 그레이디언트 손실에 10배 가중치를 부여한다.
WGAN-GP모델에 가장 잘 맞는다고 알려진 Adam 옵티마이저를 사용한다.
'''
self.crtic_model.compile(
loss=[self.wasserstrin, self.wasserstrin, partial_gp_loss]
, optimizer = Adam(lr=self.critic_learing_rate, beta_1 = 0.5)
, loss_weights = [1, 1, self.grad_weigt]
)| WGAN-gp에서 배치 정규화 WGAN-gp을 구축하기 전에 마지막으로 언급할 한 가지는 비평자에서 배치 정규화를 사용해서는 안된다는 것이다. 배치 정규화는 같은 배치 안의 이미지 사이에 상관관계(correlation)를 만들기 때문에 그레이디언트 페널티 손실의 효과가 덜어진다. 실험을 해보면 비평자에서 배치 정규화를 사용하지 않더라도 WGAN-gp이 여전히 훌륭한 결과를 만든다는 것을 알 수 있다. |
4. 생성결과
왼쪽이 보통의 GAN의 식별 함수, 오른쪽이 Wasserstein거리를 이용한 WGAN이다. 네트워크는 어느쪽도 DCGAN을 이용하고 있다.

WGAN의 쪽은 학습초기 검은 화면부터 뭉게 뭉게 결과를 출력하고 있다. WGAN의 쪽이 흐릿한 이미지가 출력된다고 알려져 있듯, 이 결과에서도 그러한 형태로 출력되고 있다. 알고리즘을 개선하여 조금 더 깨끗하게 이미지를 생성하여보았다. 그 결과는 아래의 그림과 같다.

5. WGAN-gp의 구현
(1) discriminator의 학습을 위한 모델 정의
discriminator의 학습을 위한 전체 구조(discriminator_with_own_loss)를 구현해보록 한다.

WGAN-gp의 학습에서는, 식별에 잘 사용되는 형식 (y_true, y-pred), 즉 '정답 라벨과 예상결과를 함께'와 같은 형식을 사용하지 않는다. binary_cross_entropy등의 미리 정의된 함수를 사용하는 것이 아니라 손실함수를 단독을 정의해야할 필요가 있다.
1) 손실함수를 정의하는데 사용한다.
손실함수를 독자적으로 정의하고, opromizer에 전달해 학습시키는 순서는 아래와 같다.
① model를 작성한다.
② 손실함수를 정의한다.
③ optimizer를 인스탄스화하여, updates 메소드에서 학습하는 가중치를 정의한다.
④ 입력, 출력, 인스턴스화한 optimizer를 인수로써 함수화한다.
아래에, 코드와 함께 순서대로 설명했다.
def build_discriminator_with_own_loss(self):
# 1. モデルの作成
# generatorの入力
z = Input(shape=(self.z_dim,))
# discriimnatorの入力
f_img = self.generator(g_input)
img_shape = (self.img_rows, self.img_cols, self.channels)
r_img = Input(shape=(img_shape))
e_input = K.placeholder(shape=(None,1,1,1))
a_img = Input(shape=(img_shape),\
tensor=e_input * img_input + (1-e_input) * g_output)
# discriminatorの出力
f_out = self.discriminator(f_img)
r_out = self.discriminator(r_img)
a_out = self.discriminator(a_img)
##モデルの定義終了
# 2. 損失関数の作成
# original critic loss
loss_real = K.mean(r_out)
loss_fake = K.mean(f_out)
# gradient penalty
grad_mixed = K.gradients(a_out, [a_img])[0]
norm_grad_mixed = K.sqrt(K.sum(K.square(grad_mixed), axis=[1,2,3]))
grad_penalty = K.mean(K.square(norm_grad_mixed -1))
# 最終的な損失関数
loss = loss_fake - loss_real + GRADIENT_PENALTY_WEIGHT * grad_penalty
# 3. optimizerをインスタンス化
training_updates = Adam(lr=1e-4, beta_1=0.5, beta_2=0.9)\
.get_updates(self.discriminator.trainable_weights,[],loss)
# 4. 入出力とoptimizerをfunction化
d_train = K.function([img_input, g_input, e_input],\
[loss_real, loss_fake], \
training_updates)
return d_train
① model를 작성한다.
discriminator의 학습시의 model구조(위 그림의 전체 구조)를 disciriminator_with_own_loss라고 이름을 붙였다.
이 구성의 인풋은
- generator의 잠재변수 z
- 실제 이미지의 입력 r_img
- 생성 데이터와 위조 데이터의 비율을 결정하는 e_input
이다. z는 generator에서 위조 데이터 f-img로 변환된다.
다음은 f-img와 r-img를 묶은 직선상의 임의의 점 a-img를 정의한다. 점의 위치는 파라미터 epsilon에서 조정한다. 이러한 3개의 입력을 discriminator를 통해, 각각 출력시켜, f_out, r_out, a_out을 얻는다.
② 손실함수를 정의한다.
정의에 따라, 손실함수를 선언한다. 기울기를 취하는 곳이 있지만, 미분되는 함수, 미분을 하는 변수를 헷갈리지 않도록 한다.

③ optimizer를 인스턴스화하여, updates 메소드에서 학습하는 가중치를 정의한다.
Adam optimizer를 인스턴스화하고, training_updates변수에 저장한다. get_updates메소드의 인수에는
- 학습 대상의 가중치
- 학습시의 제약조건
- 손실 함수
를 지정한다. 제약조건은 없기 때문에 빈 리스트를 지정한다.
④ 입력, 출력, 인스턴스화한 optimizer를 인수로써 함수화한다.
function 함수에 입력해주면 된다. 메소드를 정의하고 있기 때문에 return에서 반환해준다.
(cf) 차이점
지금까지의 코드에서는 입력과 출력에 대해
model = Model(input, output)
model.compile(optimizer= Adam(0.0001, beta_1=0.5, beta_2=0.9),\
loss = 'binary_crossentropy')
model.train_on_batch(input, y_true)과 같이 model을 정의하여, compile메소드를 이용, optimizer과 loss를 지정하여, trian_on_batch메소드에서 학습하고 있다. 이 방법의 경우, train_on_batch메소드에 반드시 입력과 정답 라벨을 입력할 필요가 있다.
이와 같은 개념으로 WGAN-gp의 코드를 작성한 예시가 있지만, 손실함수의 기재가 약간 오묘하기 때문에 위의 코드로 생성된 이미지는 흐리거나 별로 좋지 않다.
지금부터 다양한 알고리즘을 구현하데에 손실함수를 명식적으로 표시하는 쪽이 좋다고 생각하여, 이번에 그렇게 구현하도록하였다.
(2) generator의 학습을 위한 모델 정의
아래의 그림과 같이 작성혔다. discriminator과 같다.

def build_combined2(self):
z = Input(shape=(self.z_dim,))
img = self.generator(z)
valid = self.discriminator(img)
model = Model(z, valid)
model.summary()
loss = -1. * K.mean(valid)
training_updates = Adam(lr=1e-4, beta_1=0.5, beta_2=0.9)\
.get_updates(self.generator.trainable_weights,[],loss)
g_train = K.function([z],\
[loss], \
training_updates)
return model, g_train
(3) 인스턴스의 초기화
# combinedモデルの学習時はdiscriminatorの学習をFalseにする
for layer in self.discriminator.layers:
layer.trainable = False
self.discriminator.trainable = False
self.netG_model, self.netG_train = self.build_combined2()
# discriminator_with_ow_lossモデルの学習時はgeneratorの学習をFalseにする
for layer in self.discriminator.layers:
layer.trainable = True
for layer in self.generator.layers:
layer.trainable = False
self.discriminator.trainable = True
self.generator.trainable = False
self.netD_train = self.build_discriminator_with_own_loss()generator, discriminator의 각 학습에 대해, 학습하지 않는 곳은 고정한다.
(4) 전체의 학습시
for epoch in range(epochs):
for j in range(TRAINING_RATIO):
# ---------------------
# Discriminatorの学習
# ---------------------
# バッチサイズ分のノイズをGeneratorから生成
noise = np.random.normal(0, 1, (batch_size, self.z_dim))
gen_imgs = self.generator.predict(noise)
# バッチサイズ分の本物画像を教師データからピックアップ
idx = np.random.randint(0, X_train.shape[0], batch_size)
imgs = X_train[idx]
# discriminatorを学習
epsilon = np.random.uniform(size = (batch_size, 1,1,1))
errD_real, errD_fake = self.netD_train([imgs, noise, epsilon])
d_loss = errD_real - errD_fake
# ---------------------
# Generatorの学習
# ---------------------
noise = np.random.normal(0, 1, (batch_size, self.z_dim))
# Train the generator
g_loss = self.netG_train([noise])discriminator_with_own_loss, combined에 정의한 K.function에 대해, 입력 값을 지정한다. return값으로 output에 지정한 loss값이 리턴되기 때문에, 이것을 변수로 받는다. 변수로 받는 목적은 그 값을 플롯하기 위한 것이지만, 그 때 학습이 실행되고 있는다. (이 설명이 틀렸다면 알려주세요.)
전체 코드는 github에 공개하였다.
(4) 생성이미지
DCGAN의 결과와 같이 잠재변수의 차원을 바꿔 이미지를 생성한다.
처음은 z_dim = 100이다.

z_dim = 50

z_dim = 10

저번 포스팅에서 보였던 진동이나 같은 숫자가 생성되는 것과 같은 상황은 없다.
z_dim= 5

z_dim= 2

z_dim=1

역시 여기까지하면 완전히 모드 붕괴가 되고 있다는 것을 알 수 있다. 같은 이미지가 생성되고 있다는 것을 알 수 있다. 잠재공간의 차원가 낮으면, WGAN를 이용하여도 표현력이 낮아진다.
참고자료
https://haawron.tistory.com/21
'IT > AI\ML' 카테고리의 다른 글
| 머신러닝 정밀도의 향상을 위해 해야할 것 (0) | 2020.05.24 |
|---|---|
| [python] 교차검증(cross validation/クロスバリデーション/交差検証)과 그 방법들 (0) | 2020.05.19 |
| GAN ; 잠재 변수와 생성 이미지 (0) | 2020.05.01 |
| [논문] GAN ; CycleGAN (Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks) (2) | 2020.04.30 |
| [python] GAN; cGAN(conditional GAN) (2) | 2020.04.30 |