※ 일본의 한 블로그 글을 번역한 포스트입니다. 오역 및 의역, 직역이 있을 수 있으며 틀린 내용이 있으면 지적해주시면 감사하겠습니다.
시작하기에 앞서
이번 포스트에서는 Python의 수치 분석 라이브러리인 SciPy의 interpolate.interp2d 클래스를 사용해 2차원 형태의 데이터를 보간하는 방법에 대해서 해설하도록 하겠다.
보간의 옵션이나 실제 보간 예에 대해서 다룰 것이다. 또한, SciPy에서 interpolate.interp2d와 동일하게 2차원 데이터를 보간하는 interpolate.griddata도 있지만, 이것은 함수이다.
interp2d 클래스
interpolate.interp2d 클래스는 다음과 같이 정의되어 있다.
interp2d(x, y, z, kind='linear', copy=True,
bounds_error=False, fill_value=None)각각의 인수는 아래와 같다.
- x, y: 데이터의 좌표(1차원 배열)(1次元配列)
- z: 데이터(2차원배열)
- kind: 보간방법(linear(디폴트), cubic, quintic)
- copy: 데이터를 복사(False의 경우는 데이터의 어드레스를 참고)
- bounds_error: True의 경우, 보간시의 입력 좌표가 x, y의 범위를 넘으면 에러를 반환하며, False의 경우 범위외의 값은fill_value에서 설정한 값을 반환한다.
- fill_value: 외삽영역에 대해서 삽입할 값. None(디폴트)의 경우, 최근방법에 의한 값을 반환한다.
보간을 이용해 값을 구하고 싶은 경우는 아래와 같이 interp2d 인스턴스 f에 구하고 싶은 좌표 xnew, ynew를 전달한다. 여기서 xnew, ynew는 스칼라, 1차원 배열, 2차원배열 관계 없이 가능하다.
f = interpolate.interp2d(x, y, z, kind='cubic')
znew = f(xnew, ynew)데이터 좌표 x,y는 동일한 간격이 아니어도 괜찮다.
보간방법
interpolate.interp2d 클래스의 kind 옵션으로 지정 가능한 보간 방법으로 아래의 세 가지가 있다.
- linear: 선형 보간
- cubic: 3차 보간
- quintic: 5차 보간
linear: 선형 보간
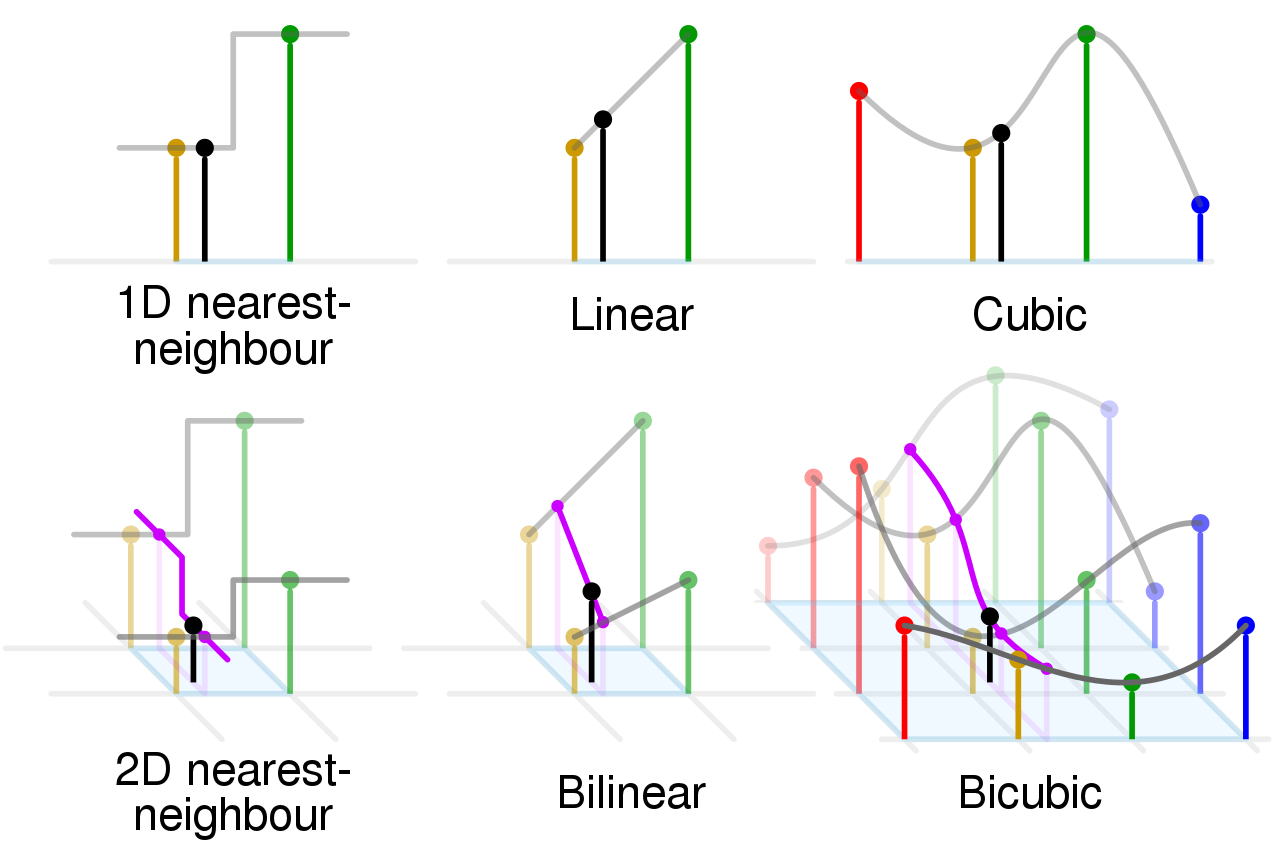
linear에는 쌍선형(bilinear) 이라는 방법으로 데이터를 보간한다(아래의 그림을 참고하길 바란다). 쌍선형 보간으로는 대상이 되는 좌표의 근방의 4개의 점을 이용하여 선형근사를 통해 값을 구한다. 이미지와 같이 먼저 x 좌표에서 2개의 점을 이용해 선형 보간을 한다. 그 후에 그 결과를 이용해 y 축 좌표를 기준으로 선형 보간을 한다.
cubic : 3차보간
cubic에서는 쌍3차(bicubic)이라는 방법을 통해 데이터 보간을 한다(아래의 그림을 참조하길 바란다). 쌍3차보간에는 대상이 되는 좌표의 근방 16개의 점 데이터를 이용해 3차근사로 값을 구한다. 이미지에서 알 수 있듯, 먼저 x좌표를 따라 4개의 점 데이터로 3차보간을 한다. 그 결과를 바탕으로 y축을 따라 다시 3차보간을 한다.
quintic
quintic은 위에서 언급했듯, 5차 근방을 이용해 값을 구한다.
2차원 데이터의 보간 예
실제로 2차원 데이터를 보간해보자.
먼저, 라이브러리를 import해서 플롯용 함수 plot2d 를 정의한다.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
def plot2d(X, Y, Z, title):
fig, ax = plt.subplots()
mappable = ax.pcolor(X, Y, Z, vmin=-1, vmax=1, shading="nearest")
fig.colorbar(mappable, ax=ax)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title(title)
fig.tight_layout()
plt.show()여기서는 아래의 두 변수를 함수를 이용해 보간한다.
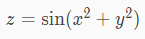
참고로 이 함수를 -6 ≤ x,y ≤ 6의 범위로 0.1씩 플롯하면 다음과 같이된다.
x = np.linspace(-3, 3, 61)
y = x.copy()
X, Y = np.meshgrid(x, y)
Z = np.sin(X**2 + Y**2)
plot2d(X, Y, Z, "original")
다음으로 보간에 이용할 데이터로 동일한 범위의 0.4씩 플롯한 수치를 준비했다.
x2 = np.linspace(-3, 3, 16)
y2 = x2.copy()
X2, Y2 = np.meshgrid(x2, y2)
Z2 = np.sin(X2**2 + Y2**2)
plot2d(X2, Y2, Z2, "rough")
linear
linear으로 선형 보간한 결과는 다음과 같다.
f_linear = interpolate.interp2d(X2, Y2, Z2, kind='linear')
Z_linear = f_linear(x, y)
plot2d(X, Y, Z_linear, "linear")
cubic
cubic으로 3차보간한 결과이다. 원래 데이터에 가까운 형태로 결과가 된다.
f_cubic = interpolate.interp2d(X2, Y2, Z2, kind='cubic')
Z_cubic = f_cubic(x, y)
plot2d(X, Y, Z_cubic, "cubic")
quintic
quintic으로 5차보간한 결과는 다음과 같인데, 이 결과도 원래 데이터와 가까운 결과가 된다.
f_quintic = interpolate.interp2d(X2, Y2, Z2, kind='quintic')
Z_quintic = f_quintic(x, y)
plot2d(X, Y, Z_quintic, "quintic")
참고자료
'IT > 언어' 카테고리의 다른 글
| [python/openCV] openCV로 도형그리기 (0) | 2022.08.10 |
|---|---|
| [python/openCV] 가로세로 비율을 유지한 채로 이미지를 리사이즈하기(이미지 사이즈 변경) (0) | 2022.08.08 |
| [python] python의 datetime으로 날짜, 시간 ⇔ 문자형 데이터 변환(strtime, strptime) (0) | 2022.07.31 |
| [python] 순서를 지정할 수 있는 dictionary ; OrderedDict의 사용법 (0) | 2022.07.26 |
| [python] 시간을 10분 단위로만 기록되도록 하기(시간 내림) (0) | 2022.07.24 |