Open3D는 3D데이터를 다루는 소프트 웨어의 개발을 서포트하는 오픈 소스 라이브러리이다. Open3D는 C++와 Python 프론트엔드를 제공하고 있으며, 엄선된 데이터 구조와 알고리즘을 두 환경에서 이용가능하다. 공식 사이트는 여기를 참고하길 바란다.
이번 포스팅에서는 이 라이브러리를 이용해서 point cloud를 3D mash(.obj, .ply, .stl, .gltf)로 변경하는 일련의 프로세스에 대해 설명하고자 한다.

데이터를 로드하여 준비하기
라이브러리를 import한다.
import numpy as np
import open3d as o3d데이터가 저장되어 있는 파일의 경로를 작성한다.
input_path="your_path_to_file/"
output_path="your_path_to_output_folder/"
dataname="sample.xyz"
point_cloud= np.loadtxt(input_path+dataname,skiprows=1)마지막으로, point_cloud 변수 타입을 numpy에서 Open3D의 o3d.geometry.PointCloud 타입으로 변환하여 처리한다.
input_path="your_path_to_file/"
output_path="your_path_to_output_folder/"
dataname="sample.xyz"
point_cloud= np.loadtxt(input_path+dataname,skiprows=1)로드한 데이터를 시각화하기 위해서는 아래의 코드를 이용한다.
o3d.visualization.draw_geometries([pcd])이것으로 pcd의 point cloud를 메쉬화하면 표면 재구축 프로세스를 시작할 준비가 됐다. 효과적인 결과를 얻는 방법에 대해 소개하겠지만, 구체적으로 설명하기 전에, 기초가 되는 프로세스를 파악하기 위한 몇 가지 세부 전략이 필요하다. 포스팅의 저자의 경우 두 가지 메쉬 전략을 사용하였다.
두 가지 전략
[전략1] Ball-Pivoting Algorithm(BPA)
Ball-Pivoting Algorithm(BPA)의 배후에 있는 방법은 가상의 Ball을 사용하여 point cloud를 메쉬로 생성하는 것을 시뮬레이션하는 것이다. 맨 처음에 전달된 point cloud가 오브젝트의 표면으로 부터 샘플링된 점으로 구성되어 있다고 가정한다. 포인트는 재구축된 메쉬가 명시적으로 표면(노이즈 프리)를 엄밀하게 나타낼 필요가 있다는 것이다.

이 상정을 사용해, point cloud의 "표면"을 가로질러 작은 Ball을 굴리는 것을 상상해자. 이 작은 Ball은 메쉬의 스케일에 의존하며, 포인트 간의 평균 공간보다 약간 더 커야할 필요가 있다. 포인트의 표면에 Ball을 떨어트리면 Ball이 걸려 시드 삼각형을 형성하는 세 개의 포인트에 자리잡는다. F의 ROM 그 위치, 두 개의 점으로 부터 형성된 삼각형의 엣지에 따라 Ball이 구른다. 다음에 Ball이 새로운 장소에 떨어진다. 전의 두 개의 꼭지점으로 부터 새로운 삼각형이 형성되어, 1개의 새로운 삼각형 메쉬가 추가된다. Ball을 굴리는 것을 반복해 새로운 삼각형이 형성되고, 메쉬에 추가된다. 메쉬가 완전히 형성되기 전까지 계속해서 Ball을 굴린다.
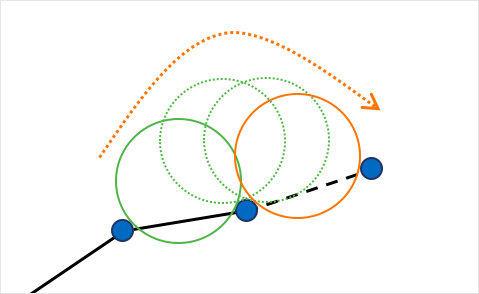
Ball-Pivoting Algorithm(BPA)의 구상 자체는 단순하지만, 주의 점이 있다.
- Ball의 반경을 어떻게 선택할까? 반경은 입력 point cloud의 사이즈와 스케일을 바탕으로 획득된다. 논리적으로는 Ball의 직경이 point간의 평균 거리보다 살짝 크게 할 필요가 있다.
- 어떤 부분에서는 point간의 거리가 너무 떨어져 있어서 Ball이 떨어져 버린 경우에 어떻게 될까? Ball이 엣지를 따라 회전하면 표면 상의 적당한 포인트를 놓쳐 버리게 되고, 대신에 다른 포인트 정확히는 세 개의 이전 포인트를 건드리게 될 가능성이 있다. 이 경우에는 새로운 삼각형 Facet의 Vertex법선(법선;주어진 객체의 수직인 선)이 점의 법선과 일관된 방향인지를 확인한다. 일관되지 않은 방향이면 생성을 거부하고 구멍을 만든다.
- 표면과 표면 간의 거리가 Ball 사이즈보다 작아지는 것과 같은 표면 주름 혹은 구멍이 있는 경우에는 어떻게 되는가? 이 경우 Ball은 주름을 무시하게 된다. 그러나 정확하지 않은 메쉬가 생성되게 되므로 좋지는 않다.
- Ball이 영역간을 제대로 구르지 못 하는 것과 같이, 포인트 영역 사이에 간격을 두고 배치되어 있는 경우는 어떻게 되는가? 가상의 Ball이 다양한 장소에 여러 번 표면에 드롭된다. 이로 인해, 포인트의 간격이 일정하지 않은 경우에도 Ball이 메쉬 전체를 캡처되는 것이 보증된다.

이 5개의 이미지는 Ball 반경에 따라 어느정도 달라지는 나타낸 것이다. 최적의 메쉬가 최적의 Geometry와 삼각형 수 균형을 자동적으로 획득하고 있는 것을 알 수 있다.
[전략2] 푸아송 재구성
푸아송 재구성은 조금더 기술적 수학적이다. 이 접근법은 암묵적인 메쉬 방법으로 알려져 있는데, 매끄러운 천으로 데이터를 "감싸는 것"으로 설명할 수 있다. 너무 상세 내용으로 들어가진 않겠다. 법선에 링크된 등치면을 나타내는 새로운 포인트 세트를 작성하여 원래의 포인트 세트와 밀접하게 표면으로 적합되도록 한다. 메쉬의 결과에 영향을 끼칠 가능성이 있는 몇 가지 파라미터가 있다.
- 깊이는 어느정도로 하면 좋은가? 수목의 깊이는 재구축에 사용된다. 메쉬가 높을 수록 상세하게 된다(기본은 8). 노이즈가 많은 데이터를 사용하면, 생성된 메쉬에 반하는 꼭지점이 유지된지만 알고리즘은 그만큼 탐색하지 않는다. 따라서 최저값(5에서 7의 사이의 값)은 스무싱 효과를 제공하지만, 상세한 표현은 놓치고 만다. 심도값이 높을수록, 생성된 메쉬의 꼭지점의 결과양이 많아진다.

- 폭은 어느정도로 하면 좋은가? 이것은 팔진 트리라고 불리는 트리 구조의 최고 레벨의 타겟 폭을 지정한다. 이것과 3D의 최적의 데이터 구조에 대해서는 이 포스팅의 범위를 넓히기 때문에, 설명은 생략하도록 하겠다. 아무튼 깊이가 지정된 경우 이 파라미터는 무시된다.
- 스케일은 어느정도로 하는 것이 좋은가? 이것은 재구성에 사용된 입방체의 직경과 샘플의 경계 입방체의 직경의 비교를 나타낸다. 매우 추상적이며, 기본 파라미터 설정도 꽤 잘 기능한다.

스케일 파라미터의 결과를 나타낸 이미지이다.
예제 코드
먼저, 포인트 간의 모든 거리를 계산한 평균 거리를 바탕으로 필요한 반경 파라미터를 계싼한다.
distances = pcd.compute_nearest_neighbor_distance()
avg_dist = np.mean(distances)
radius = 3 * avg_distbpa_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(pcd,o3d.utility.DoubleVector([radius, radius * 2]))dec_mesh = mesh.simplify_quadric_decimation(100000)dec_mesh.remove_degenerate_triangles()
dec_mesh.remove_duplicated_triangles()
dec_mesh.remove_duplicated_vertices()
dec_mesh.remove_non_manifold_edges()* 주의 : 이 전략은 Open3D 버전 0.9.0.0부터 이용할 수 있다.
푸아송으로 결과를 얻는 것은 매우 간단하다. 위와 같이 함수에 전달할 파라미터를 조정할 필요가 있다.
poisson_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(pcd, depth=8, width=0, scale=1.1, linear_fit=False)[0]깔끔한 결과를 얻기 위해서는 아래의 왼쪽 이미지의 노란 색 부분, 즉 불필요한 부분을 제거하기 위해서는 트리밍 추가할 필요가 있다.

그렇게 하기 위해서 원래의 point cloud를 포함한 초기 경계 박스를 계산하고 그 값을 사용해 경계 박스 외의 모든 표면을 필터링한다.
bbox = pcd.get_axis_aligned_bounding_box()
p_mesh_crop = poisson_mesh.crop(bbox)이제 결과를 export하고 시각화하자. write_triangle_mesh함수를 사용하면 데이터의 export를 간단히 할 수 있다. 작성한 파일의 이름, .ply, .obj, .stl, 혹은 .gltf 중 필요한 확장자 및 그리고 export할 메시를 선택하면 된다. 아래에서는 BPA와 푸아송으로 재구성한 것 둘 다를 .ply 파일로 export하고 있는 코드이다.
o3d.io.write_triangle_mesh(output_path+"bpa_mesh.ply", dec_mesh)
o3d.io.write_triangle_mesh(output_path+"p_mesh_c.ply", p_mesh_crop)def lod_mesh_export(mesh, lods, extension, path):
mesh_lods={}
for i in lods:
mesh_lod = mesh.simplify_quadric_decimation(i)
o3d.io.write_triangle_mesh(path+"lod_"+str(i)+extension, mesh_lod)
mesh_lods[i]=mesh_lod
print("generation of "+str(i)+" LoD successful")
return mesh_lodsmy_lods = lod_mesh_export(bpa_mesh, [100000,50000,10000,1000,100], ".ply", output_path)my_lods2 = lod_mesh_export(bpa_mesh, [8000,800,300], ".ply", output_path)o3d.visualization.draw_geometries([my_lods[100]])마지막으로 이것을 임의의 3D 인쇄 소프트웨어에 import하면 다음과 같이 확인할 수 있다.

참고자료
'IT > 언어' 카테고리의 다른 글
| [python] python으로 csv파일 쓰기 (list, numpy, pandas) (0) | 2022.02.21 |
|---|---|
| [python/Matplotlib] 3차원 데이터 가시화(표시) (0) | 2022.01.17 |
| [python] 오브젝트의 속성을 조작하는 delattr/getattr/hasattr/setattr (0) | 2022.01.13 |
| [python/OpenCV] cv2.Canny():Canny방법을 이용하여 물체의 외곽선(엣지) 추출하기 (2) | 2022.01.04 |
| [python/Numpy] 분산을 계산하는 var()의 사용법과 주의법 (0) | 2021.12.24 |