머신 러닝 공부 중 설명 변수와 목적 변수에 대한 내용이 있어 한 번 정리해보고자 한다.
설명 변수와 목적변수
간단히 정의하자면 설명 변수와 목적 변수를 다음과 같이 정리할 수 있을 것 같다.
- 목적 변수 : 기계학습의 교사 학습(Supervised learning)에 있어서 예측하고 싶은 정보
- 설명 변수 : 기계학습의 교사 학습(Supervised learning)에 있어서 예측에 사용하는 정보
- 모델 : 설명 변수와 목적 변수를 결합하는 "상자'(함수나 프로그램)
동의어는 다음과 같다.
| 목적 변수 | 설명 변수 |
| - 종속 변수(Dependent variable) - 반응 변수(Response variable) - 결과 변수(Outcome variable) - 표적 변수(Target variable) |
- 독립 변수(Independent variable) - 예측 변수(Predictor variable) - 회귀자(Regressor) - 원인 변수 - 조작 변수(mulipulated variable) - 통제 변수(controlled variable) - 노출 변수(exposure variable) - 리스크 팩터(risk factor) - 특징(feature) (기계학습) - 공변량(Covariate) (연속형 자료) - 요인(Factor) (범주형 자료) - 입력 변수(input variable) |
구체적인 예를 들자면 다음과 같다.
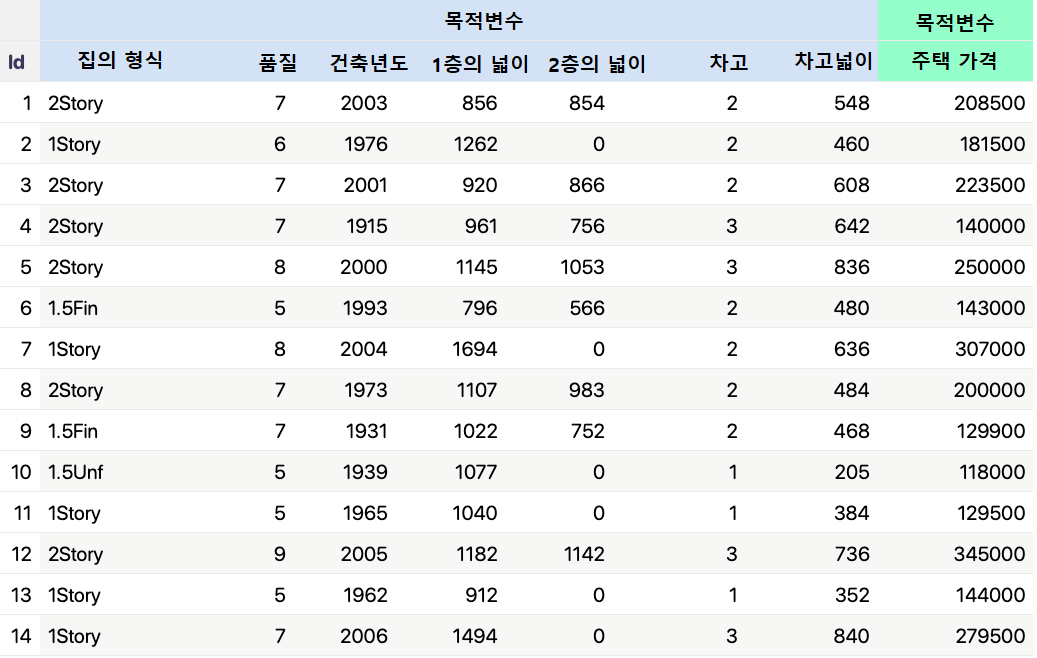
건물의 가격을 예측하는 기계학습 모델을 만들 구상을 하고 있을 때, 교사 학습의 예로써 다음과 같은 데이터가 준비되어 있다고 가정하자.
이때에, 가격은 목적 변수이다. 또한 가격에 영향을 주는 즉 목적 변수 이외의 모든 변수는 설명 변수가 된다.
목적 변수에 따른 문제의 종류
목적 변수에 따라 문제의 종류가 달라진다.
- 목적 변수가 수치(숫자)인 경우 회귀 문제 ([예] 판매 예측)
- 목적 변수가 ID형태인 경우 분류 분제 ([예] 클릭 예측 ("클릭함" 혹은 "클릭하지 않음") )
교사 학습 - 회귀
선형 회귀 분석(linear regression)이외에는 비선형 분석(nonlinear regression)이다.
선형 회귀에서는 선형 파라미터가 필요하지만, 비선형회귀에서는 필요하지 않다. 선형 파라미터와의 관계를 적절히 모델화할 수 없는 경우에는 선형회귀가 아닌 비선형회귀를 사용한다.
선형회귀분석
회귀의 경우, 목적 변수 : 설명 변수의 그래프를 이으면 선이 된다.

MARS(Mutivariate adaptive regression splines)
부분적으로 선형 모델을 만들고 있는 느낌이다.

서포트 벡터 회귀(SVR)
서포트 벡터 머신의 아이디어를 이용하고 있다.
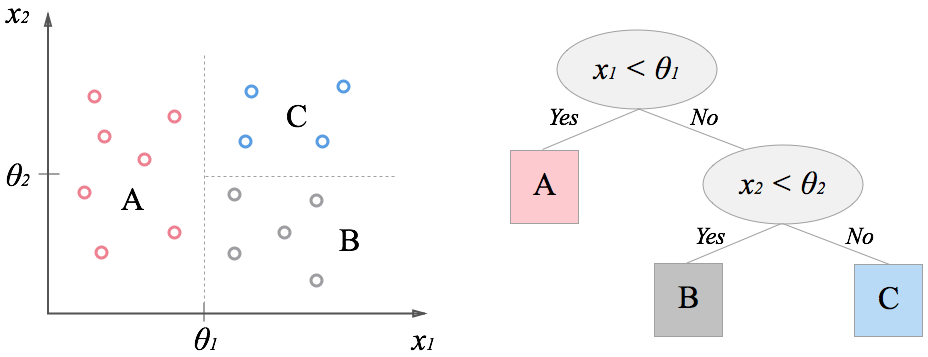
회귀 나무
트리형으로 분류해간다. 잎의 평균값이 나뭇가지의 값이된다. 이산적인 값만 예측 할 수 없다. 데이터가 그룹으로 분리된다.
나무 모형
나무 모형은 회귀 나무와 비슷하지만, 회귀 나무가 예측값으로써 단말 노드의 평균값을 이용하는 반면, 나무 모형의 경우는 선형 회귀 모델으로 에측값을 구한다.
유전자 프로그래밍
어떤 모델로 할 것인지 측정한다. 진화론과 비슷하다. 최초로 적당한 난수로 비구조를 만들어 이걸 대상으로 연산한다. 시행 횟수가 적으면 좋은 결과를 얻을 수 없다.

교사 학습 - 분류
이진분류
심플한 방법. 데이터를 두 종류로 분류한다.
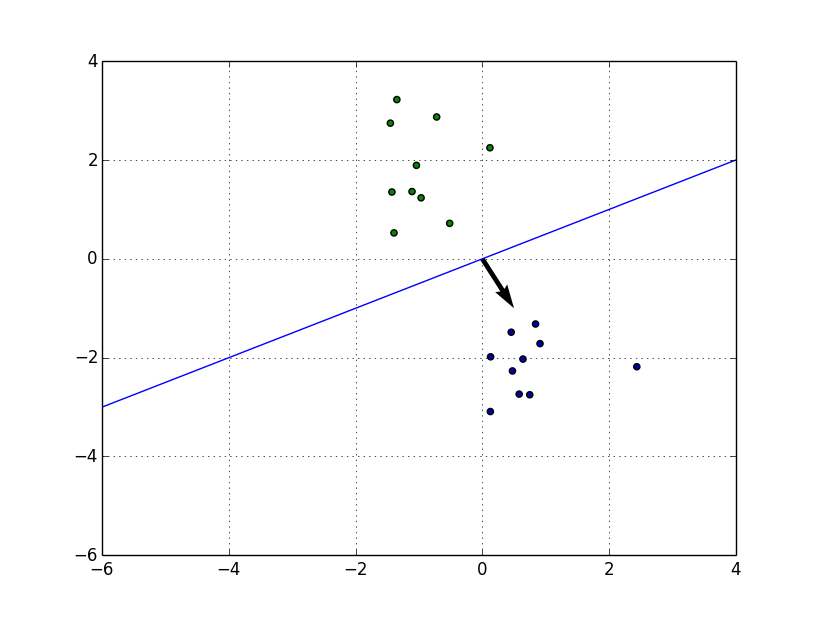
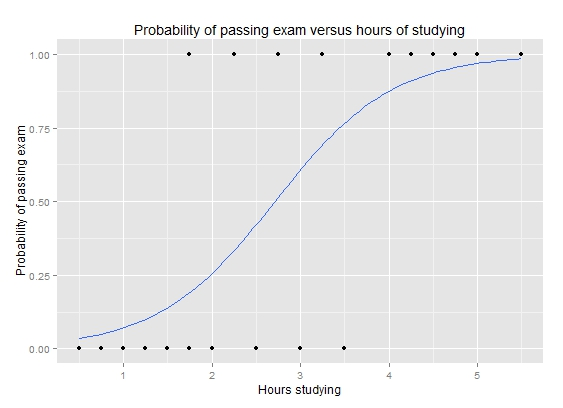
로지스틱 회귀
선형 대신에 시그모이드 곡선(S자형태의 곡선)을 이용한 회귀 방법
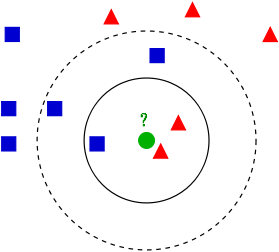
K 평균 군집
학습 데이터를 벡터 공간상에 블록해두고, 미지의 데이터를 뿌린 후 그 공간으로부터의 거리가 가까운 순서대로 임의의 데이터 K개를 취득한다. 그리고 다수결로 데이터가 속해 있는 클래스를 측정한다.
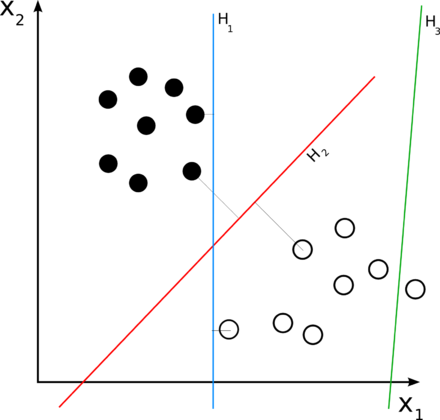
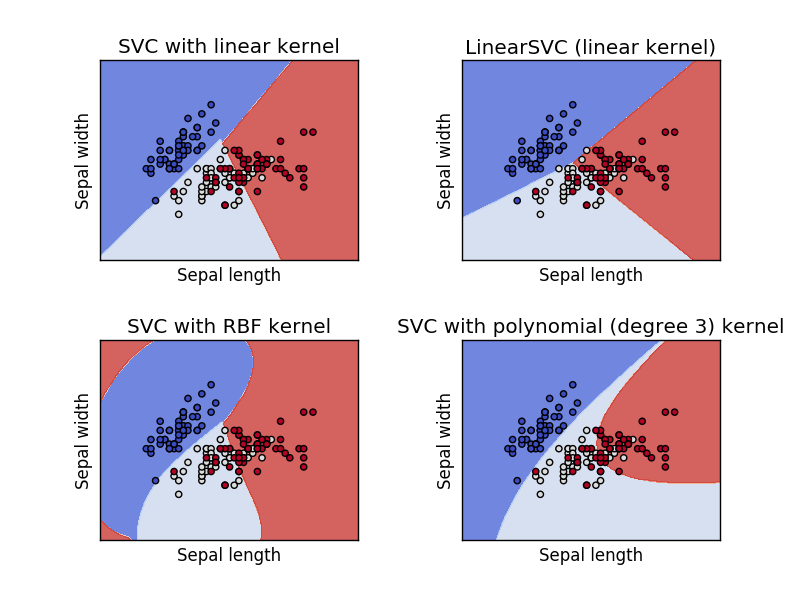
서포트 벡터 머신(SVM)
커넬 함수를 이용한 선형 분리가 되지 않은 것을 특정 공간에 맵핑하여 분리할 수 있도록 하고 있다. 커넬의 종류는 네 가지가 있다(linear, polynomial, rbf, sigmoid).
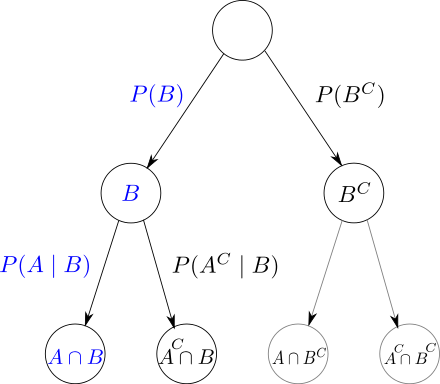
결정 트리
트리형으로 분류
랜덤 포레스트
나무 형태가 제각각인 나무를 많이 만든다. 예측할 때는 다수결로한다. 분류 정답률이 높지만, 왜 이러한 결과가 되었는지 이유를 분명히 알 수 없다는 것이 단점이다.
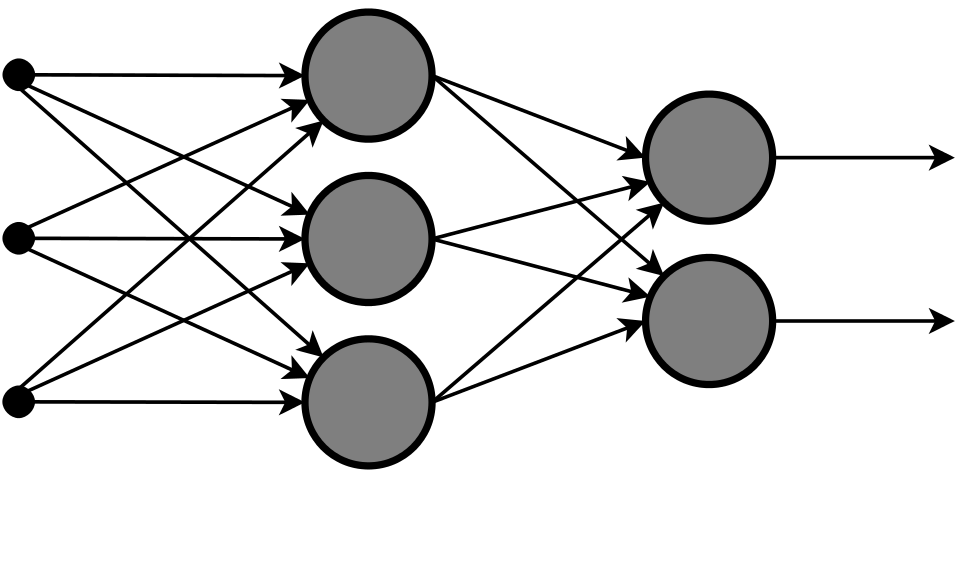
뉴럴 네트워크
인간의 뇌 신경회로의 특성을 계산기 상의 시뮬레이션을 이용해 표현한 것을 의미하는 수학 모델이다.
참고자료
https://zzanhtt.tistory.com/53
https://www.varista.ai/knowledge/objective-and-explanatory-variables/
https://qiita.com/t-yotsu/items/1a6bf3a4f3242eae7857
'IT > AI\ML' 카테고리의 다른 글
| [python/openCV] openCV로 이미지 여백 삭제 (1) (0) | 2021.07.06 |
|---|---|
| 카테고리 변수를 다루는 네 가지 방법 (0) | 2021.06.03 |
| ipywidgets 사용법 (2) (2) | 2021.04.07 |
| ipywidgets 사용법 (1) (0) | 2021.04.06 |
| [논문] 최근 AI의 이미지 인식에서 화제인 "Vision Transformer"에 대한 해설 (0) | 2020.10.16 |