문제 링크
https://github.com/yoyoyo-yo/Gasyori100knock/tree/master/Question_31_40
yoyoyo-yo/Gasyori100knock
画像処理100本ノックして画像処理を画像処理して画像処理するためのもの For Japanese, English and Chinese - yoyoyo-yo/Gasyori100knock
github.com
Q31. 아핀 변환-스크류(アフィン変換、スキュー)
(1) 아핀변환을 이용하여, 출력(1)과 같이 X-sharing(dx = 30)이미지를 만들어보자.
(2) 아핀변환을 이용하여, 출력(2)과 같이 Y-sharing(dy = 30)이미지를 만들어보자.
(3) 아핀 변환을 이용하여, 출력(3)과 같이 기하 변환한 (dx = 30, dy = 30) 이미지를 만들어보자.
이러한 이미지들을 스크류 이미지라고 부르기도 하며,
이미지를 비스듬한 방향에 위치하도록 하는 것이다.
출력(1)의 경우, x방향으로 dx정도 움직인 이미지를 X-sharing으로 부르며,
출력(2)의 경우, y방향으로 dy정도 움직인 이미지를 Y-sharing이라고 부른다.
위 두 방식 모두 아핀변환으로 실현가능하다.
다만, 원본 이미지의 사이즈는h x w이다.
(1) X-sharing

(2) Y-sharing

A31. 아핀 변환-스크류(アフィン変換、スキュー)의 답안
import cv2
import numpy as np
import matplotlib.pyplot as plt
# Affine
def affine(img, dx=30, dy=30):
# get shape
H, W, C = img.shape
# Affine hyper parameters
a = 1.
b = dx / H
c = dy / W
d = 1.
tx = 0.
ty = 0.
# prepare temporary
_img = np.zeros((H+2, W+2, C), dtype=np.float32)
# insert image to center of temporary
_img[1:H+1, 1:W+1] = img
# prepare affine image temporary
H_new = np.ceil(dy + H).astype(np.int)
W_new = np.ceil(dx + W).astype(np.int)
out = np.zeros((H_new, W_new, C), dtype=np.float32)
# preprare assigned index
x_new = np.tile(np.arange(W_new), (H_new, 1))
y_new = np.arange(H_new).repeat(W_new).reshape(H_new, -1)
# prepare inverse matrix for affine
adbc = a * d - b * c
x = np.round((d * x_new - b * y_new) / adbc).astype(np.int) - tx + 1
y = np.round((-c * x_new + a * y_new) / adbc).astype(np.int) - ty + 1
x = np.minimum(np.maximum(x, 0), W+1).astype(np.int)
y = np.minimum(np.maximum(y, 0), H+1).astype(np.int)
# assign value from original to affine image
out[y_new, x_new] = _img[y, x]
out = out.astype(np.uint8)
return out
# Read image
img = cv2.imread("assets/imori.jpg").astype(np.float32)
# Affine
out = affine(img, dx=30, dy=30)
# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)<numpy.ceil()>
올림 함수이다. 입력의 요소 단위의 ceil값을 반환한다.
스칼라 x의 ‘ceil’는 x보다 크거나 같은, 가장 작은 정수이다.
흔히 ⎡x⎤로 표현된다.
numpy.ceil(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'ceil'>
- x : array_like
- out:ndarray, None, or tuple of ndarray and None, optional
- where : array_like, optional
** kwargs
> 리턴값 :ndarray 또는 scalar
http://codetorial.net/numpy/functions/numpy_ceil.html
https://docs.scipy.org/doc/numpy/reference/generated/numpy.ceil.html
http://labs.eecs.tottori-u.ac.jp/sd/Member/oyamada/OpenCV/html/py_tutorials/py_imgproc/py_geometric_transformations/py_geometric_transformations.html
Q32. 푸리에 변환(フーリエ変換)
이차원이산푸리에변환(DFT)을 적용해, imori.jpg을 흑백화시킨 것의 주파수의 파워 스펙트럼을 표시해보자. 그리고 역이차원이산푸리에(IDFT)로 이미지를 복원해보자.
이차원이산푸리에변환(DFT: Discrete Fourier Transformation)은 푸리에 변환의 이미지에 대해 처리 방법이다. 보통의 푸리에변환은 아날로그 신호나 음성 등의 연속값이자 1차원을 대상으로 주파성분을 구하는 계산처리이다.
한편, 디지털 이미지는 [0,255]의 이산값을 가지고 있으며 이미는 HxW의 2차원으로 표시되기 때문에, 2차원 이산 푸리에 변환이 사용 가능하다.
K = [0, W-1], l = [0, H-1], 입력이미지를 I로 한다면, 2차원 이산 푸리에 변환(DFT)는 다음의 식으로 계산된다.
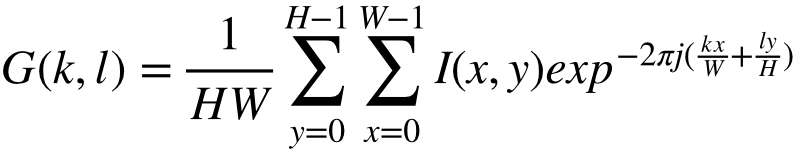
여기에서는 이미지를 흑백화한 다음에 2차원이산푸리에 변환을 적용하라.
파워 스펙트럼이란 G가 복소수로 표시되는 것이므로, G의 절대값을 구해야한다.
이번에만 이미지 표시를 할 때 파워 스펙트럼을 [0,255]으로 스케일링하자.
역 2차원 이산 푸리에 변환 (IDFT: Inverse DFT)은 주파수 성분 G에서 부터 원래의 이미지를 복원하는 방법으로,
다음의 식으로 정의되어 있다.
x = [0, W-1], y = [0, H-1]
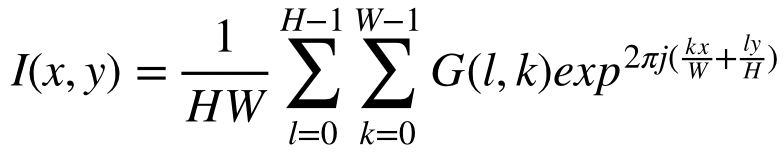
위의 정의식에서 exp(j)는 복소수의 값을 얻게 되므로
실제 코드를 작성할 때는 아래의 식처럼 절대값을 사용한다.
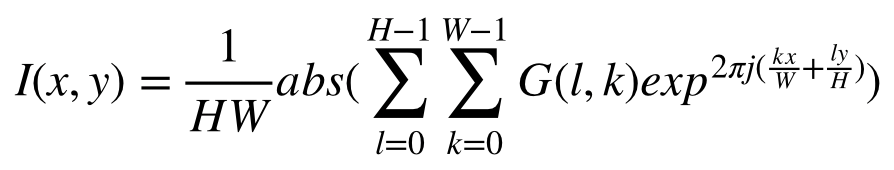
간단하게 전부 반복문을 돌리면 128^4의 계산이 되므로 시간이 걸린다.
numpy을 잘 활용하면 계산에 소요되는 비용을 감소시킬 수 있다.
(해답은 128^2까지 비용을 감소시켰다.)
A32. 푸리에 변환(フーリエ変換)의 답안
import cv2
import numpy as np
import matplotlib.pyplot as plt
# DFT hyper-parameters
K, L = 128, 128
channel = 3
# DFT
def dft(img):
H, W, _ = img.shape
# Prepare DFT coefficient
G = np.zeros((L, K, channel), dtype=np.complex)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# dft
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
#for n in range(N):
# for m in range(M):
# v += gray[n, m] * np.exp(-2j * np.pi * (m * k / M + n * l / N))
#G[l, k] = v / np.sqrt(M * N)
return G
# IDFT
def idft(G):
# prepare out image
H, W, _ = G.shape
out = np.zeros((H, W, channel), dtype=np.float32)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# idft
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# Read image
img = cv2.imread("assets/imori.jpg").astype(np.float32)
# DFT
G = dft(img)
# write poser spectal to image
ps = (np.abs(G) / np.abs(G).max() * 255).astype(np.uint8)
cv2.imwrite("out_ps.jpg", ps)
# IDFT
out = idft(G)
# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)
"""
fimg = np.fft.fft2(gray)
# 第1象限と第3象限, 第2象限と第4象限を入れ替え
fimg = np.fft.fftshift(fimg)
print(fimg.shape)
# パワースペクトルの計算
mag = 20*np.log(np.abs(fimg))
# 入力画像とスペクトル画像をグラフ描画
plt.subplot(121)
plt.imshow(gray, cmap = 'gray')
plt.subplot(122)
plt.imshow(mag, cmap = 'gray')
plt.show()
"""<numpy.exp()>
입력된 배열의 요소들을 자연상수 e 인 지수함수 로 변환해준다.
https://docs.scipy.org/doc/numpy/reference/generated/numpy.exp.html
<numpy.sqrt()>
음수가 아닌 배열의 제곱근 요소를 반환한다.
https://docs.scipy.org/doc/numpy/reference/generated/numpy.sqrt.html
Q33. 푸리에 변환 - 로우패스 필터 (フーリエ変換 ローパスフィルタ)
흑백화한 imori.jpg를 DFT하여, 로우패스필터를 통해 IDFT로 이미지를 복원해보자. DFT에 따라 얻어지는 주파수성분은 좌상, 우상, 좌하, 우하에 가까울수록 저주파수의 성분을 포함하고 있다는 의미이며, 중심에 가까울수록 고주파 성분이라는 것을 의미한다.

이미지에서 고주파 성분은 색이 변한 부분(노이즈나 윤곽 등)을 나타내며 저주파 성분과 색상이 별로 변하지 않은 부분(석양의 그라데이션 등)을 나타낸다. 여기에서는 고주파 성분은 차단하고, 저주파 성분만을 통과하는 로우패스 필터를 적용해보자. 저주파 수의 중심에서 고주파까지의 거리를 r로 하면 0.5r까지의 성분을 통과시킨다고 한다.
A33. 푸리에 변환 - 로우패스 필터 (フーリエ変換 ローパスフィルタ)의 답안
import cv2
import numpy as np
import matplotlib.pyplot as plt
# DFT hyper-parameters
K, L = 128, 128
channel = 3
# bgr -> gray
def bgr2gray(img):
gray = 0.2126 * img[..., 2] + 0.7152 * img[..., 1] + 0.0722 * img[..., 0]
return gray
# DFT
def dft(img):
# Prepare DFT coefficient
G = np.zeros((L, K, channel), dtype=np.complex)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# dft
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
#for n in range(N):
# for m in range(M):
# v += gray[n, m] * np.exp(-2j * np.pi * (m * k / M + n * l / N))
#G[l, k] = v / np.sqrt(M * N)
return G
# IDFT
def idft(G):
# prepare out image
H, W, _ = G.shape
out = np.zeros((H, W, channel), dtype=np.float32)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# idft
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# LPF
def lpf(G, ratio=0.5):
H, W, _ = G.shape
# transfer positions
_G = np.zeros_like(G)
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# get distance from center (H / 2, W / 2)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# make filter
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
mask = np.ones((H, W), dtype=np.float32)
mask[r > (W // 2 * ratio)] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# filtering
_G *= mask
# reverse original positions
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
# Read image
img = cv2.imread("assets/imori.jpg").astype(np.float32)
H, W, C = img.shape
# Gray scale
gray = bgr2gray(img)
# DFT
G = dft(img)
# LPF
G = lpf(G)
# IDFT
out = idft(G)
# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)(cf)푸리에 변환에 대해서
삼각함수의 Sin파를 떠올려보자. 아래와 같은 그림이 그려질 것이다.

이 그림의 위쪽을 보자면 아래와 같은 줄무늬가 된다.

조셉 푸리에는 이 줄무늬의 방향을 변환하여 포개는(덧셈) 것으로, 어떤 이미지를 표현할 수 있다는 사실을 발견했다.
그것에 대한 내용은 아래의 링크의 슬라잇 62페이지 부터 82페이지를 참고하라.
https://www.slideshare.net/ginrou799/ss-46355460
33번의 로우패스 필터는 줄무늬 맵(주파수 공간)에서 작은 줄무늬를 지우는 것이다. 일반적으로 작은 줄무늬는 아래 이미지의 점들(노이즈)로 나타나는 경향이 있으므로 로우패스 필터를 적용하면

아래와 같은 이미지가 된다. 노이즈 부분이 감소되는 것을 확인할 수 있다.

반대로 하이패스 필터(자잘한 줄무늬를 남기는) 처리에 대해 얘기하자면, 이미지 중에 있는 점(작은 점들)을 검출하고 싶을 때 등에 사용할 수 있다. 다른 예도 있다. 낮은 주파수를 마릴린 먼로의 이미지, 높은 주파수를 아이슈타인 이미지로 만들어 겹치면 아래와 같이 된다.

이 이미지는 가까이에서 보자면 아이슈타인(높은 주파수)로 보이지만 멀리서 보자면 마릴린 먼로(낮은 주파수)로 보인다.이것은 멀리 떨어지면 사람은 높은 주파수를 볼 수 없게 되기 때문이다. 가까이서 나무(높은 주파수)를 보면 숲(낮은 주파수)이 보이지 않게 되는데, 멀리서 숲(낮은 주파수)을 보면 나무(높은 주파수)가 보이지 않는 것과 같다.
Q34. 푸리에 변환 - 하이패스 필터 (フーリエ変換 ハイパスフィルタ)
imori.jpg를 흑백화한 것을 DFT하여 하이패스필터를 통해 IDFT로 이미지를 복원해보자.
여기에서는 저주파성분을 자르고, 고주파 성분만 통과하는 하이패스 필터를 적용한다.
여기에서는 저주파 수의 중심부터 고주파 까지의 거리 r이라고 한다면 0.1r부터의 성분을 통과하게 하는 것이다.
A34. 푸리에 변환 - 하이패스 필터 (フーリエ変換 ハイパスフィルタ) 의 답안
import cv2
import numpy as np
import matplotlib.pyplot as plt
# DFT hyper-parameters
K, L = 128, 128
channel = 3
# bgr -> gray
def bgr2gray(img):
gray = 0.2126 * img[..., 2] + 0.7152 * img[..., 1] + 0.0722 * img[..., 0]
return gray
# DFT
def dft(img):
# Prepare DFT coefficient
G = np.zeros((L, K, channel), dtype=np.complex)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# dft
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
#for n in range(N):
# for m in range(M):
# v += gray[n, m] * np.exp(-2j * np.pi * (m * k / M + n * l / N))
#G[l, k] = v / np.sqrt(M * N)
return G
# IDFT
def idft(G):
# prepare out image
H, W, _ = G.shape
out = np.zeros((H, W, channel), dtype=np.float32)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# idft
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# HPF
def hpf(G, ratio=0.1):
H, W, _ = G.shape
# transfer positions
_G = np.zeros_like(G)
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# get distance from center (H / 2, W / 2)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# make filter
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
mask = np.ones((H, W), dtype=np.float32)
mask[r < (W // 2 * ratio)] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# filtering
_G *= mask
# reverse original positions
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
# Read image
img = cv2.imread("assets/imori.jpg").astype(np.float32)
H, W, C = img.shape
# Gray scale
gray = bgr2gray(img)
# DFT
G = dft(img)
# HPF
G = hpf(G)
# IDFT
out = idft(G)
# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)Q35. 푸리에 변환 - 밴드 패스 필터 (フーリエ変換 バンドパスフィルタ)
imori.jpg을 흑백화한 것을 DFT하여, 하이패스 필터를 통해 IDFT로 이미지를 복원하자.
여기서는 저주파 성분과 고주파 성분의 중간 주파수 성분만을 통화하는 하이 패스 필터를 적용해보자.
여기에서는 저주파 수의 중심에서 부터 고주파 까지의 거리 r라고 한다면 0.1r부터 0.5r까지의 성분만 통과하도록 하는 것이다.
A35. 푸리에 변환 - 밴드 패스 필터(フーリエ変換 バンドパスフィルタ)의 답안
import cv2
import numpy as np
import matplotlib.pyplot as plt
# DFT hyper-parameters
K, L = 128, 128
channel = 3
# bgr -> gray
def bgr2gray(img):
gray = 0.2126 * img[..., 2] + 0.7152 * img[..., 1] + 0.0722 * img[..., 0]
return gray
# DFT
def dft(img):
# Prepare DFT coefficient
G = np.zeros((L, K, channel), dtype=np.complex)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# dft
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
#for n in range(N):
# for m in range(M):
# v += gray[n, m] * np.exp(-2j * np.pi * (m * k / M + n * l / N))
#G[l, k] = v / np.sqrt(M * N)
return G
# IDFT
def idft(G):
# prepare out image
H, W, _ = G.shape
out = np.zeros((H, W, channel), dtype=np.float32)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# idft
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# BPF
def bpf(G, ratio1=0.1, ratio2=0.5):
H, W, _ = G.shape
# transfer positions
_G = np.zeros_like(G)
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# get distance from center (H / 2, W / 2)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# make filter
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
mask = np.ones((H, W), dtype=np.float32)
mask[(r < (W // 2 * ratio1)) | (r > (W // 2 * ratio2))] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# filtering
_G *= mask
# reverse original positions
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
# Read image
img = cv2.imread("assets/imori.jpg").astype(np.float32)
H, W, C = img.shape
# Gray scale
gray = bgr2gray(img)
# DFT
G = dft(img)
# BPF
G = bpf(G, ratio1=0.1, ratio2=0.5)
# IDFT
out = idft(G)
# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)(cf) 푸리에 변환 OpenCV
<목표>1) OpenCV를 사용하여 이미지를 푸리에 변환하는 방법을 배운다
2) Numpy의 FFT의 사용방법을 배운다.
3) 푸리에 변환을 사용한 어플리케이션에 대해 배운다.
4) cv2.dft(), cv2.idft()과 같은 함수의 사용 방법을 배운다.
1. 이론
푸리에 변환은 다양한 필터의 주파수 특성을 해석하기 위해 사용된다. 이미지에 대해서는 2차원 이산 푸리에 변환 DFT을 사용하여 주파수 영역으로 변환한다. 고속화된 알고리즘인 고속 푸리에 변환 FFT은 DFT의 계산에 사용된다. 이들 알고리즘에 관련된 자세한 내용은 신호처리나 이미지처리의 교습서를 참고하라. 사인파를 아래와 같이 쓴다.

여기서 f는 신호의 주파수를 표현한 것이다. 만약 이 신호를 주파수 영역으로 관측한다면, 주파수 f의 점에는 spike가 보인다. 이산신호를 형성하기 위한 신호를 표준화라고 한다면, 같은 주파수 영역에서의 신호를 얻을 수 있으나, 주파수영역에의 신호는 [- pi, pi]의 범위나[0, 2파이]의 범위에서의 주기성을 가진 신호로 간주된다. (N점 DFT이면 [0,N]의 범위)
이미지는 2방향의 표준화한 신호로 간주할 수 있다. 그러므로 수평 방향과 수직 방향에 푸리 변환을 계산하면, 이미지를 주파수 영역으로 표현할 수 있다. 더 직관적으로 말하자면, 어떤 사인파 신호의 진폭 변화가 단시간에 빨리 일어나면 고주파 신호라고 하며, 진폭 변화가 느리면 저주파 신호라고 부르는데 이 아이디어를 이미지에 적용해보자. 이미지 중에서 진폭변환가 급격하게 발생하는 곳은 어디일까? 그것은 바로 엣지나 노이즈이다. 즉, 엣지나 노이즈는 이미지의 고주파 성분이라고 할 수 있다. 진폭의 변화가 크면 크지 않다면 저주파 성분이 된다. 이제 푸리에변환의 계산 방법을 보자.
2. Numpy를 사용한 푸리에 변환
처음에는 Numpy를 사용한푸리에 변환 계산 방법을 살펴보자. Numpy는 FFT를 계산하기 위해 함수 np.fft.fft2()를 사용한다. 이 함수는 복소수형의 배열이 리턴된다. 제1 인수는 입력 이미지를 흑백화한 것이여야 하며, 제 2인수는 출력 배열의 사이즈를 지정하는 것이나 옵션이다. 지정하는 사이즈가 입력이미지의 사이즈보다 크게 되면 입력 이미지는 FFT의 계산을 하기 전에 제로 패딩된다. 입력 이미지의 사이즈보다 작게 입력하면 이미지가 잘리게 된다. 아무것도 입력하지 않으면 입력 이미지와 같은 사이즈로 출력된다.
실제로 계산을 해보면, 저주파영역의 원점(직류 성분)이 이미지의 좌우의 각에 위치하게 된다.직류 성분을 이미지 중심으로 이동하기 위해서는 스펙트럼 전체를 N/2양방향으로 반드시 옮겨야 한다. 그러한 이동에는 np.fft.ffshift() 함수를 사용한다. (이것으로 분석이 더 쉽게 된다.) 한 번 푸리에 변환을 계산해보면, 스펙트럼의 크기를 알 수 있다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('messi5.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()결과는 아래와 같다.:

중심에 하얀색 영역이 집중되어 있는 것을 알 수 있다. 이것은 이미지가 저주파 성분을 보다 많이 포함하고 있다는 의미이다. 이것으로 푸리에 변환을 한 번 살펴보았다. 이것으로 하이패스필터와 같은 주파수영역으로의 처리가 가능해졌다. 저주파 성분에 대해 직사각형 윈도우를 사용한 마스크 처리를 하게 되어 저주파 성분을 제거할 수 있다. 그리고 np.ifftshift()함수를 사용하여 직류 성분의 위치를 이미지의 왼쪽 상단에 되돌리고 나서 np.ifft2()함수를 사용하여 역 푸리에 변환을 적용해보자. 최종적으로 결과는 복소수형의 배열이 되므로, 절대값을 취해야한다.
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)
plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(img_back, cmap = 'gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()결과는 아래와 같다:

결과를 보자면, 하이패스필터로 인해 이미지의 중심의 엣지가 검출될 수 있음을 알 수 있다.
이것은 이미지의 경사의 튜토리얼에서 보았던 결과 그 자체이다.
이미지의 대부분의 성분이 저주파 영역에 존재한다는 것도 알 수 있다.
아무튼 Numpy를 사용한 이산 푸리에 변환 DFT, 역 이산 푸리에 변환 IDFT을 배었다.
다음은 OpenCV를 사용한 방법을 배워보자.
결과를 주의 깊게 관측하면, 특히 JET색으로 묘사된 최종의 이미지를 볼 때, 유사 윤곽(빨간색 화살표로 표시된 부분)이 있다는 사실을 알 수 있다.
파도 같은 구조로 보이는데, 이것을 링깅 효과라고 부른다.
직사각형 윈도우를 사용하여 마스크 처리한 것이 원인이다.
이 마스크는 푸리에 변환에 따라 sinc함수가 되기 때문에 이런 결과가 되어버린 것 이다.
그러므로 직사각형 윈도우는 필터링에서는 사용하지 않는다.
필터링은 Gaussian윈도우 등이 더욱 적합하다.
3. OpenCV를 사용한 푸리에 변환
OpenCV에서는 DFT를 할 때에는 cv2.dft()를 사용하며, IDFT에서는 cv2.idft()를 사용한다.
Numpy와 같이 부동소수점 형의 배열이 리턴된다는 점을 동일하지만, 2채널의 배열이다.
최초의 채널은 결과의 실부, 두 번째이 채널은 허부에 대응하고 있다.
입력 이미지는 np.float32형으로 변환할 필요가 있다.
그렇다면 어떻게 계산되는지 보자.
import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('messi5.jpg',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()<노트>
cv2.cartToPolar()함수를 사용해 진폭과 위상 둘 다를 얻었다.
다음은 IDFT이다. 전 섹션에서 하이패스 필터를 시도했기 때문에, 여기에서는 로우패스 필터(고주파 성분의 제거)를 실시해본다.
로우 패스 필터는 이미지에 흐름을 추가한다.
처음에는 저주파영역에 높은 값을 가지고, 고주파 영역이 0이 되는 마스크를 작성한다.
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()결과를 살펴 보면 아래와 같다:

<노트>
언제나 마찬가지로, OpenCV 함수에 있는 cv.2dft()와 cv.idft()는 Numpy의 처리보다 빠르다.
그러나 Numpy의 함수는 다루기 수운 인터페이스를 제공한다.
퍼포먼스에 대해서는 다음의 장에 설명되어 있다.
4. DFT의 퍼포먼스 최적화
DFT의 포퍼먼스를 최적화하기 위한 배열 사이즈가 있다. 그것은 바로 배열의 사이즈가 2의 제곱일 경우이다. 배열의 사이즈가 2,3,5의 곱으로 표시되는 경우에도 효율적으로 계산된다 자신의 구현이 불안할 경우에는 DFT를 적용하기 전에 배열의 사이지를 제로 패딩 등을 사용하여 최적화된 사이즈로 변경하는 것이 좋다. OpenCV를 사용하는 것에 있어 제로패딩은 수동으로 적용해야 할 필요가 있다.
한편, Numpy에서는 FFT를 계산할 때에 배열의 사이즈를 지정하면 제로 패딩이 적용된다.최적화된 값을 어떻게 계산하는 것이 좋을까? OpenCV가 제공하고 있는 cv2.getOptimalDFTSize()함수를 사용한다. cv2.dft()와 np.fft.fft2()함수 어느 쪽도 사용할 수 있다. IP y 라고 n의 magic command인 %timeit을 사용해 퍼포먼스를 조사해보자.
In [16]: img = cv2.imread('messi5.jpg',0)
In [17]: rows,cols = img.shape
In [18]: print rows,cols
342 548
In [19]: nrows = cv2.getOptimalDFTSize(rows)
In [20]: ncols = cv2.getOptimalDFTSize(cols)
In [21]: print nrows, ncols
360 576배열의 사이즈가 (342, 548)에서 (360, 576)로 변경되는 것을 알 수 있겠는가. 제로 패딩부터 DFT을을 해보자. 제로 패딩을 하기 위해서는 전 요소의 값이 0인 새로운 배열을 사용해, 원래의 이미지 데이터를 복사한다.
nimg = np.zeros((nrows,ncols))
nimg[:rows,:cols] = imgcv2.copyMakeBorder()함수를 사용하여도 제로 패딩이 가능하다.
right = ncols - cols
bottom = nrows - rows
bordertype = cv2.BORDER_CONSTANT #just to avoid line breakup in PDF file
nimg = cv2.copyMakeBorder(img,0,bottom,0,right,bordertype, value = 0)드디어 DFT를 계산할 수 있게 되었다. Numpy의 함수와의 퍼포먼스를 비교해보자
In [22]: %timeit fft1 = np.fft.fft2(img)
10 loops, best of 3: 40.9 ms per loop
In [23]: %timeit fft2 = np.fft.fft2(img,[nrows,ncols])
100 loops, best of 3: 10.4 ms per loop4배 정도 빨라지게 되었다. 동일한 성능 계측을 OpenCV에서도 해보자.
In [24]: %timeit dft1= cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT)
100 loops, best of 3: 13.5 ms per loop
In [27]: %timeit dft2= cv2.dft(np.float32(nimg),flags=cv2.DFT_COMPLEX_OUTPUT)
100 loops, best of 3: 3.11 ms per loop여기서도 4배 정도 빨라졌다.
OpenCV함수를 사용하면 Numpy의 함수를 사용할 때보다 3배 정도 빠르게 계산 결과가 나온다는 것을 알 수 있다.
역 푸리에 변환도 이와 같이 테스트해보자.
6. 왜 Laplacian이 하이패스 필터일까?
포럼에도 비슷한 질문이 들려왔다. 질문은 '왜 Laplacian필터가 하이패스 필터일까? 왜 Sobel필터가 하이패스 필터가 아닐까?'이다. 그에 대한 첫번째 대답은 푸리에 변환부터 설명하도록 하면서 하도록 하겠다. Laplacian필터의 푸리에 변환을 계산하고 해석해보자.
import cv2
import numpy as np
from matplotlib import pyplot as plt
# simple averaging filter without scaling parameter
mean_filter = np.ones((3,3))
# creating a guassian filter
x = cv2.getGaussianKernel(5,10)
gaussian = x*x.T
# different edge detecting filters
# scharr in x-direction
scharr = np.array([[-3, 0, 3],
[-10,0,10],
[-3, 0, 3]])
# sobel in x direction
sobel_x= np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
# sobel in y direction
sobel_y= np.array([[-1,-2,-1],
[0, 0, 0],
[1, 2, 1]])
# laplacian
laplacian=np.array([[0, 1, 0],
[1,-4, 1],
[0, 1, 0]])
filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \
'sobel_y', 'scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
for i in xrange(6):
plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()결과는 아래와 같다:

결과 이미지를 보자면, 각 커넬이 어떤 주파수대혁을 차단하는지, 어떤 주파수대가 통과하는지 알 수 있다.
여기서부터 상기의 모델에서 시험한 커넬은 하이패스 필터 혹은 로퍼스 필터 어느쪽이 될지 알 수 있다.
'IT > AI\ML' 카테고리의 다른 글
| [python/Tensorflow2.0] Mnist 학습 모델 (2)-CNN;Sequential, Functional, Model Subclassing (0) | 2020.04.20 |
|---|---|
| [python/Tensorflow2.0] Mnist 학습 모델 (1)-DNN(Deep Neural Network) (0) | 2020.04.20 |
| [python/OpenCV] 이미지 처리 예제 Q26~Q30 (0) | 2020.04.20 |
| [python/OpenCV] 이미지 처리 예제 Q21~Q25 (0) | 2020.04.20 |
| [python/OpenCV] 이미지 처리 예제 Q16~Q20 (0) | 2020.04.20 |